Quantum Gates

Introduction

Import the modules

from qiskit import QuantumCircuit, execute, Aer

from qiskit import QuantumRegister, ClassicalRegister #The newer version uses Registers

from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import pi

a = 0
b = 1
t = 2

Plot the quantum circuit

qc.draw('mpl')
#qc.draw('latex')
#qc.draw('latex_source')

Plot the results

backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
qc.measure_all()
qc.draw()
result = execute(qc,backend).result()  #.get_statevector()  #.get_counts()
plot_bloch_multivector(result)

counts = result.get_counts()
plot_histogram(counts)

Theory

Quantum Gates of One Qubit

There are only two reversible gates, also identity (return the input unchanged) and NOT (return the opposite of the input), but neither is universal.

Identity gate.

Pauli X gate. $\sigma _{x}=X={\begin{bmatrix}0&1\\1&0\end{bmatrix}}=|0\rangle \langle 1|+|1\rangle \langle 0|$

Pauli Y gate $\sigma _{y}=Y={\begin{bmatrix}0&-i\\i&0\end{bmatrix}}=-i|0\rangle \langle 1|+i|1\rangle \langle 0|$

Pauli Z gate $\sigma _{z}=Z={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}=|0\rangle \langle 0|-|1\rangle \langle 1|$

Hadamard gate $H={\tfrac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}=|+\rangle \langle 0|+|-\rangle \langle 1|$

R gate $R_{\phi }={\begin{bmatrix}1&0\\0&e^{i\phi }\end{bmatrix}}$

S gate or ${\sqrt {Z}}$ gate $S={\begin{bmatrix}1&0\\0&e^{\frac {i\pi }{2}}\end{bmatrix}}$

T gate $T={\begin{bmatrix}1&0\\0&e^{\frac {i\pi }{4}}\end{bmatrix}}$

U1 gate: $U_{1}=U_{3}(0,0,\lambda )=U_{1}={\begin{bmatrix}1&0\\0&e^{i\lambda }\\\end{bmatrix}}$

U2 gate: $U_{2}=U_{3}({\tfrac {\pi }{2}},\phi ,\lambda )={\tfrac {1}{\sqrt {2}}}{\begin{bmatrix}1&-e^{i\lambda }\\e^{i\phi }&e^{i\lambda +i\phi }\end{bmatrix}}$

qc = QuantumCircuit(1)
qc.x(0)
#qc.y(0) # Y-gate on qubit 0
#qc.z(0) # Z-gate on qubit 0
#qc.rz(pi/4, 0)
#qc.s(0)   # Apply S-gate to qubit 0
#qc.sdg(0) # Apply Sdg-gate to qubit 0
qc.t(0)   # Apply T-gate to qubit 0
qc.tdg(0) # Apply Tdg-gate to qubit 0

Two Qubit Quantum Gates

The reversibel gates are eg. identity, or CNOT.

Eg. $X\otimes H={\begin{bmatrix}0&H\\H&0\end{bmatrix}}$.

CNOT gate as a pictoram.

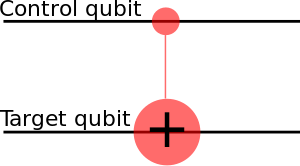
Eg. CNOT is a conditional gate that performs an X-gate on the second qubit, if the state of the first qubit (control) is $|1\rangle$. $CNOT={\begin{bmatrix}1&0&0&0\\0&0&0&1\\0&0&1&0\\0&1&0&0\\\end{bmatrix}}$. This matrix swaps the amplitudes of |01⟩ and |11⟩ in the statevector. ${\text{CNOT}}(x,y)=(x,x\otimes y)$.

CNOT if a control qubit is on the superposition:

${\text{CNOT}}|{-}0\rangle =|{-}0\rangle$

${\text{CNOT}}|{-}1\rangle =-|{-}1\rangle$

${\text{CNOT}}|0{+}\rangle ={\tfrac {1}{\sqrt {2}}}(|00\rangle +|11\rangle )$, which is Bell State. Entanglement, but no-communication theorem.

${\text{CNOT}}|{+}{+}\rangle =|{+}{+}\rangle )$. Unchanged.

${\text{CNOT}}|{-}{+}\rangle ={\tfrac {1}{\sqrt {2}}}(|{-}0\rangle -|{-}1\rangle )=|{-}{-}\rangle$

${\text{CNOT}}|{+}{-}\rangle =$.

${\text{CNOT}}|{-}{-}\rangle ={\tfrac {1}{2}}(|00\rangle -|01\rangle -|10\rangle +|11\rangle )=|{-}{-}\rangle$. Affects the state of the control qubit, only.

qc = QuantumCircuit(2)
qc.h(0)     # Apply H-gate to the first:
qc.cx(0,1)  # Apply a CNOT:

Any controlled quantum gate is ${\text{Controlled-U}}={\begin{bmatrix}I&0\\0&U\end{bmatrix}}$ and in Qiskit formalism is written in matrix as ${\text{Controlled-U}}={\begin{bmatrix}1&0&0&0\\0&u_{00}&0&u_{01}\\0&0&1&0\\0&u_{10}&0&u_{11}\\\end{bmatrix}}$

• 

  Controlled H

• 

  Controlled Y

• 

  Controlled Z

Controlled-Z. Because $HXH=Z$ and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H Z H = X} we can write

qc = QuantumCircuit(2)
# also a controlled-Z
qc.h(1)
qc.cx(0,1)
qc.h(1)

Controlled-Y is

qc = QuantumCircuit(2)
# a controlled-Y
qc.sdg(1)
qc.cx(0,1)
qc.s(1)

or Controlled-H is

qc = QuantumCircuit(2)
# a controlled-H
qc.ry(pi/4,1)
qc.cx(0,1)
qc.ry(-pi/4,1)

Swap gate: CNOT.

An arbitrary controlled-controlled-U for any single-qubit rotation U. We need Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \sqrt U} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V^\dagger}

#The controls are qubits a and b, and the target is qubit t.
#Subroutines cu1(theta,c,t) and cu1(-theta,c,t) need to be defined
qc = QuantumCircuit(3)
qc.cu1(theta,b,t)
qc.cx(a,b)
qc.cu1(-theta,b,t)
qc.cx(a,b)
qc.cu1(theta,a,t)

Three Qubit Gates

Toffoli gate made using CNOTs.

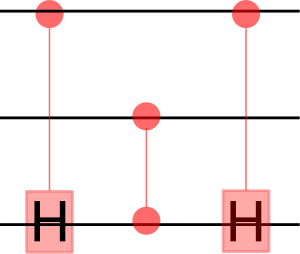
For universal computations we need more qubits. Eg. the AND gate is not reversible, and thus we need eg. Toffoli (CCNOT) gate.

Toffoli gate performs Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} on target qubit if both control cubits are set to state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1\rangle} .

qc = QuantumCircuit(3)
# Toffoli with control qubits a and b and target t
qc.ccx(a,b,t)

Toffoli using CNOTs uses fewer gates.

qc = QuantumCircuit(3)
qc.ch(a,t)
qc.cz(b,t)
qc.ch(a,t)

AND gate is Toffoli gate with . . .

The nand gate

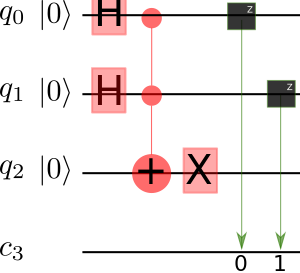
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{CCNOT}(x,y,z) = (x,y,( x \and y ) \otimes z )} gives the reversible NAND Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{NAND}(x,y) = \text{CCNOT}(x,y,1) = (x,y,( x \and y ) \otimes 1 )}

NAND gate is

Multiple Controlled Toffoli

mct()

Logical Gates

The gates must be reversible.

Not Gate

The X gate is a not gate, and is reversible.

And Gate

The classical And mixes the inputs, thus we need two inputs. The Toffoli gate will do

qc.ccx(q[0], q[1], q[2])

Nand Gate

The Nand Gate is easy after the And gate. Just apply the Not gate.

qc.ccx(q[0], q[1], q[2])
qc.x(q[2])

Xor gate

Or gate is true only if either of inputs is true. Thus we have:

qc.cx(q[1], q[2])
qc.cx(q[0], q[2])

Or Gate

The Or gate is true if either is true, thus first check the nots and then toffoli (and):

qc.cx(q[0], q[2])
qc.cx(q[1], q[2])
qc.ccx(q[0], q[1], q[2])

Nor Gate

The Nor gate is the negation of Or gate:

qc.cx(q[0], q[2])
qc.cx(q[1], q[2])
qc.ccx(q[0], q[1], q[2])
qc.x(q[2])

Half Adder --- Results

qc.initialize([1,0], 0)
qc.initialize([1,0], 1)
print(count)
-> {'00': 1000}

qc.initialize([1,0], 0)
qc.initialize([0,1], 1)
-> {'01': 1000}

qc.initialize([0,1], 0)
qc.initialize([1,0], 1)
-> {'01': 1000}

qc.initialize([0,1], 0)
qc.initialize([0,1], 1)
-> {'10': 1000}

Full Adder

The state is initialized to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle} , thus to set it to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1\rangle} we may initialize it or use X Gate.

##Define registers and a quantum circuit
q = QuantumRegister(4)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,c)

#
#qc.initialize([1,0], 0)
#qc.initialize([0,1], 1)
#qc.initialize([1,0], 2)

qc.x(q[0])
qc.x(q[2])

##AND -- carry
qc.ccx(q[0], q[1], q[3])
qc.cx(q[0], q[1])
qc.ccx(q[1], q[2], q[3])
qc.cx(q[1], q[2])
qc.cx(q[0], q[1])


##Sum
qc.measure(q[2], c[0])
##Carry out
qc.measure(q[3], c[1])

Oops 😕! Result did not match expected values Please review your answer and try again.:

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import IBMQ, Aer, execute

##Define registers and a quantum circuit
q = QuantumRegister(5)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,c)

#
qc.initialize([1,0], 0)
qc.initialize([0,0], 1)
qc.initialize([1,0], 2)


##AND -- carry
qc.ccx(q[0], q[1], q[4])
qc.ccx(q[0], q[2], q[4])
qc.ccx(q[1], q[2], q[4])
qc.barrier()


##XOR - sum
qc.cx(q[0], q[3])
qc.cx(q[1], q[3])
qc.cx(q[2], q[3])
qc.barrier()


emulator = Aer.get_backend('qasm_simulator')
job = execute(qc, emulator, shots=2048 )
hist = job.result().get_counts()
plot_histogram(hist)



##Sum
qc.measure(q[3], c[0])
##Carry out
qc.measure(q[4], c[1])

backend = Aer.get_backend('qasm_simulator')
job = execute(qc, backend, shots=1000)
result = job.result()
count =result.get_counts()
print(count)
qc.draw(output='mpl')

Results

Results for the second case:

qc.initialize([0,1], 0)
qc.initialize([0,1], 1)
qc.initialize([0,1], 2)
-> {'11': 1000}

qc.initialize([0,1], 0)
qc.initialize([0,1], 1)
qc.initialize([1,0], 2)
-> {'10': 1000}

qc.initialize([0,1], 0)
qc.initialize([1,0], 1)
qc.initialize([0,1], 2)
-> {'10': 1000}

qc.initialize([0,1], 0)
qc.initialize([1,0], 1)
qc.initialize([1,0], 2)
-> {'01': 1000}

qc.initialize([1,0], 0)
qc.initialize([0,1], 1)
qc.initialize([0,1], 2)
-> {'10': 1000}

qc.initialize([1,0], 0)
qc.initialize([0,1], 1)
qc.initialize([1,0], 2)
-> {'01': 1000}

qc.initialize([1,0], 0)
qc.initialize([1,0], 1)
qc.initialize([0,1], 2)
-> {'01': 1000}

qc.initialize([1,0], 0)
qc.initialize([1,0], 1)
qc.initialize([1,0], 2)
-> {'00': 1000}

References

https://www.quantum-inspire.com/kbase/full-adder/

https://lahirumadushankablog.wordpress.com/2020/02/04/quantum-half-adder-and-full-adder/

https://agentanakinai.wordpress.com/2019/08/31/quantum-full-adder/

https://medium.com/@sashwat.anagolum/arithmetic-on-quantum-computers-addition-7e0d700f53ae

https://docs.microsoft.com/en-us/quantum/user-guide/libraries/standard/algorithms