Pascal's Triangle

Binomial expansion

${\begin{aligned}(a+b)^{0}&=1\\(a+b)^{1}&=a+b\\(a+b)^{2}&=a^{2}+2ab+b^{2}\\(a+b)^{3}&=(a+b)(a+b)^{2}=(a+b)(a^{2}+2ab+b^{2})\\&=a^{3}+2a^{2}b+ab^{2}+ba^{2}+2ab^{2}+b^{3}\\&=a^{3}+3a^{2}b+3ab^{2}+b^{3}\\(a+b)^{4}&=\cdots \end{aligned}}$

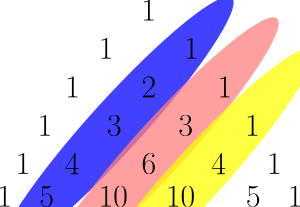
Pascal's triangle

Pascal's Triangle

The coefficients of binomial expansion can be easily seen from the Pascal triangle. The number is a sum of the two numbers above it.

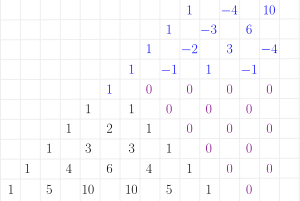
Pascal's triangle: Negative right

This can be extended to negative numbers easily.

Pascal triangle extended to negative values

Now, instead of expanding $(a+b)^{n}$, we will use $(1+x)^{n}$, where $n$ is a negative integer. The exponent of each terms grows when going to left. We get according to the Pascal triangle

${\begin{aligned}(1+x)^{-1}&=1-x+x^{2}-x^{3}+\cdots \\(1+x)^{-2}&=1-2x+3x^{2}-4x^{3}+\cdots \\(1+x)^{-3}&=1-3x+6x^{2}-\cdots \end{aligned}}$

And by Taylor series (expansion at $x=-1$Laurent series) we get

• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-1%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-2%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-3%29+%29

Pascal's triangle: Negative left

The triangle can be extended to the left also, but it is symmetric to the earlier.

Pascal's triangle: half-integers

Newton: Find the area of the curve $y={\sqrt {1-x^{2}}}=(1-x^{2})^{1/2}$, because it is a quarter of a unit circle $A={\frac {\pi }{4}}$. He couldn't do that, so he took some other powers, and calculated the areas following Wallis and Fermat method that was known:

${\begin{aligned}y_{0}&=(1-x^{2})^{0/2}=(1-x^{2})^{0}=1=&&\to &&A(y_{0})=x={\frac {1}{1}}x\\y_{1}&=(1-x^{2})^{1/2}\\y_{2}&=(1-x^{2})^{2/2}=1-x^{2}&&\to &&A(y_{2})=x-{\frac {1}{3}}x^{3}={\frac {1}{1}}x-{\frac {1}{3}}x^{3}\\y_{3}&=(1-x^{2})^{3/2}\\y_{4}&=(1-x^{2})^{4/2}=(1-x^{2})^{2}=1-2x^{2}+x^{4}&&\to &&A(y_{4})=x-{\frac {2}{3}}x^{3}+{\frac {1}{5}}x^{5}={\frac {1}{1}}x-{\frac {2}{3}}x^{3}+{\frac {1}{5}}x^{5}\\y_{5}&=(1-x^{2})^{5/2}\\y_{6}&=(1-x^{2})^{6/2}=(1-x^{2})^{3}=1-3x^{2}+3x^{4}-x^{6}&&\to &&A(y_{6})=x-x^{3}+{\frac {3}{5}}x^{5}-{\frac {1}{7}}x^{7}={\frac {1}{1}}x-{\frac {3}{3}}x^{3}+{\frac {3}{5}}x^{5}-{\frac {1}{7}}x^{7}\end{aligned}}$

Newton noted that

• the first term is always $x$. He assumed that that is true also for half-integer numbers
• The denominator is always an odd integer: $1,3,5,7,\dots$
• the second term is ${\frac {0}{3}}x^{3}$, ${\frac {1}{3}}x^{3}$, ${\frac {2}{3}}x^{3}$, ${\frac {3}{3}}x^{3}$, etc. Thus, because the numerator of the second term is separated by $1$ he assumed that when adding the half-integers into the list, the separation will be $1/2$, also $0,{\frac {1}{2}},1,{\frac {3}{2}},2,{\frac {5}{2}},3\dots$ So, this will give the the first and second term half-integer to be

${\begin{aligned}A(y_{1})&=A[(1-x^{2})^{1/2}]=x-{\frac {\tfrac {1}{2}}{3}}x^{3}+{\frac {a_{12}}{5}}x^{5}-\cdots =x-{\frac {1}{6}}x^{3}+{\frac {a_{12}}{5}}x^{5}-\cdots \\A(y_{3})&=A[(1-x^{2})^{3/2}]=x-{\frac {\tfrac {1+1}{2}}{3}}x^{3}+{\frac {a_{32}}{5}}x^{5}-\cdots =x-{\frac {1}{3}}x^{3}+{\frac {a_{32}}{5}}x^{5}-\cdots \\A(y_{5})&=A[(1-x^{2})^{5/2}]=x-{\frac {\tfrac {1+2}{2}}{3}}x^{3}+{\frac {a_{5_{2}}}{5}}x^{5}-\cdots =x-{\frac {1}{2}}x^{3}+{\frac {a_{52}}{5}}x^{5}-\cdots \end{aligned}}$

Newton argued that the coefficient $a_{12}$ must be $a_{12}={\frac {1}{2}}\times {\frac {{\tfrac {1}{2}}-1}{2}}=-{\frac {1}{8}}$ and by multiplying continously, he got the next term in $A(y_{1})$ to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{13} = -\frac18 \times \frac{\tfrac12 -2}{2} = \frac1{16} } and next Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{14} = \frac1{16} \times \frac{\tfrac12 -3}{2} = -\frac5{128} } and thus he got Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(y_1) = A[ (1-x^2)^{1/2} ] = x - \frac16 x^3 - \frac1{40}x^5 - \frac1{112}x^7 - \cdots }

Furthermore, Newton realised that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1} also can be presented as a power series: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1 = (1-x^2)^{1/2} = 1 - \frac12 x^2 - \frac18 x^4 - \frac1{16}x^6 - \cdots } and Newton multiplied it by itself, and got the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-x^2} .

Numbers

• Natural numbers
• Triangular numbers
• Tetrahedral numbers
• Pentatope numbers
• 5-simplex numbers
• 6-simplex numbers
• 7-simplex numbers

Fibonacci numbers