Pascal's Triangle

Binomial expansion

${\begin{aligned}(a+b)^{0}&=1\\(a+b)^{1}&=a+b\\(a+b)^{2}&=a^{2}+2ab+b^{2}\\(a+b)^{3}&=(a+b)(a+b)^{2}=(a+b)(a^{2}+2ab+b^{2})\\&=a^{3}+2a^{2}b+ab^{2}+ba^{2}+2ab^{2}+b^{3}\\&=a^{3}+3a^{2}b+3ab^{2}+b^{3}\\(a+b)^{4}&=\cdots \end{aligned}}$

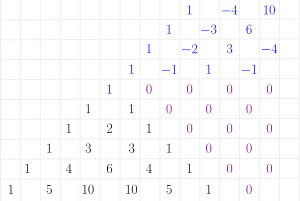
Pascal's triangle

Pascal's Triangle

The coefficients of binomial expansion can be easily seen from the Pascal triangle. The number is a sum of the two numbers above it.

Pascal's triangle: Negative right

This can be extended to negative numbers easily.

Pascal triangle extended to negative values

Now, instead of expanding $(a+b)^{n}$, we will use $(1+x)^{n}$, where $n$ is a negative integer. The exponent of each terms grows when going to left. We get according to the Pascal triangle

${\begin{aligned}(1+x)^{-1}&=1-x+x^{2}-x^{3}+\cdots \\(1+x)^{-2}&=1-2x+3x^{2}-4x^{3}+\cdots \\(1+x)^{-3}&=1-3x+6x^{2}-\cdots \end{aligned}}$

And by Taylor series (expansion at $x=-1$Laurent series) we get

• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-1%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-2%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-3%29+%29

Pascal's triangle: Negative left

The triangle can be extended to the left also, but it is symmetric to the earlier.

Pascal's triangle: half-integers

Newton: Find the area of the curve $y={\sqrt {1-x^{2}}}=(1-x^{2})^{1/2}$, because it is a quarter of a unit circle $A={\frac {\pi }{/}}4$. He couldn't do that, so he took some other powers:

${\begin{aligned}y_{0}&=(1-x^{2})^{0/2}=(1-x^{2})^{0}=1\\y_{1}&=(1-x^{2})^{1/2}\\y_{2}&=(1-x^{2})^{2/2}=1-x^{2}\\y_{3}&=(1-x^{2})^{3/2}\\y_{4}&=(1-x^{2})^{4/2}=(1-x^{2})^{2}=1-2x+x^{4}\\y_{5}&=(1-x^{2})^{5/2}\\y_{6}&=(1-x^{2})^{6/2}=(1-x^{2})^{3}=1-3x^{2}+3x^{4}-x^{6}\end{aligned}}$