Introduction Error creating thumbnail: convert-im6.q16: unrecognized color `context-fill' @ warning/color.c/GetColorCompliance/1057. convert-im6.q16: non-conforming drawing primitive definition `fill' @ error/draw.c/RenderMVGContent/4414. Dipole antennas and transmission coefficient. See the svg file Antenn system.
Lähetin, johto, antenni, jne. https://www.antenna-theory.com/tutorial/txline/transmissionline.php
https://www.worldradiohistory.com/BOOKSHELF-ARH/Technology/Rider-Books/R-F%20Transmission%20Lines%20-%20Alexander%20Schure.pdf
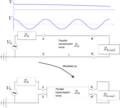
Transmission line, general case
The (long) transmission line is modeled as Z 0 . If the frequency (wavelength) of the source is too large (small) compared to dimensions of the system, it need to be considered in more detailed. See also the svg file.
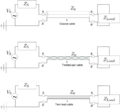
The physical realizations of the transmission lines are usually coaxial cables, twisted cables or twin lead cables.
The system is analyzed as being differential short pieces. The conductance
G
{\displaystyle G}
If a transmission line has a length greater than about 10% of a wavelength, then the line length will noticeably affect the circuit's impedance. The equation in the above image can be written as
∂
v
d
x
=
−
L
∂
i
∂
t
−
R
i
∂
i
d
x
=
−
C
∂
v
∂
t
−
G
v
{\displaystyle {\begin{aligned}{\frac {\partial v}{dx}}&=-L{\frac {\partial i}{\partial t}}-Ri\\{\frac {\partial i}{dx}}&=-C{\frac {\partial v}{\partial t}}-Gv\end{aligned}}}
and these two is easy to combine, and it gives the second degree dy
∂
2
v
d
x
2
−
L
C
∂
2
v
∂
t
2
=
(
R
C
+
G
L
)
∂
v
∂
t
+
G
R
v
{\displaystyle {\frac {\partial ^{2}v}{dx^{2}}}-LC{\frac {\partial ^{2}v}{\partial t^{2}}}=(RC+GL){\frac {\partial v}{\partial t}}+GRv}
and similar equation to i . Lets solve those.
Lossless transmission If wire resistance and insulation conductance can be neglected, the model depends only on L and C elements. Thus, we have two similar wave equations for v and i (only for v is shown)
∂
v
∂
t
2
−
v
^
2
∂
v
∂
x
2
=
0
{\displaystyle {\frac {\partial v}{\partial t^{2}}}-{\hat {v}}^{2}{\frac {\partial v}{\partial x^{2}}}=0}
where
v
^
=
(
L
C
)
−
1
/
2
{\displaystyle {\hat {v}}=(LC)^{-1/2}}
The solutions to the above equations is the sum of forward and backward traveling (reflected) waves:
v
(
z
,
t
)
=
v
+
e
−
α
z
e
ı
(
ω
t
−
γ
z
)
+
v
−
e
α
z
e
ı
(
ω
t
+
γ
z
)
{\displaystyle v(z,t)=v^{+}e^{-\alpha z}e^{\imath (\omega t-\gamma z)}+v^{-}e^{\alpha z}e^{\imath (\omega t+\gamma z)}}
α
=
0
{\displaystyle \alpha =0}
https://en.wikipedia.org/wiki/Telegrapher's_equations
v
(
z
,
t
)
=
v
+
e
ı
(
ω
t
−
γ
z
)
+
v
−
e
ı
(
ω
t
+
γ
z
)
{\displaystyle v(z,t)=v^{+}e^{\imath (\omega t-\gamma z)}+v^{-}e^{\imath (\omega t+\gamma z)}}
i
=
i
(
z
,
t
)
{\displaystyle i=i(z,t)}
i
(
z
,
t
)
=
v
+
Z
0
e
ı
(
ω
t
−
γ
z
)
+
v
−
Z
0
e
ı
(
ω
t
+
γ
z
)
=
v
+
Z
0
e
ı
(
ω
t
−
γ
z
)
(
1
−
v
−
v
+
e
ı
(
2
γ
z
)
)
{\displaystyle i(z,t)={\frac {v^{+}}{Z_{0}}}e^{\imath (\omega t-\gamma z)}+{\frac {v^{-}}{Z_{0}}}e^{\imath (\omega t+\gamma z)}={\frac {v^{+}}{Z_{0}}}e^{\imath (\omega t-\gamma z)}\left(1-{\frac {v^{-}}{v^{+}}}e^{\imath (2\gamma z)}\right)}
The fraction
v
−
v
+
{\displaystyle {\frac {v^{-}}{v^{+}}}}
Γ
{\displaystyle \Gamma }
v
−
v
+
=
Γ
e
ı
ϕ
z
=
Z
L
−
Z
0
Z
L
+
Z
0
{\displaystyle {\frac {v^{-}}{v^{+}}}=\Gamma e^{\imath \phi _{z}}={\frac {Z_{L}-Z_{0}}{Z_{L}+Z_{0}}}}
which gives
i
(
z
,
t
)
==
v
+
Z
0
e
ı
(
ω
t
−
γ
z
)
(
1
−
Γ
e
ı
(
ϕ
z
+
2
γ
z
)
)
{\displaystyle i(z,t)=={\frac {v^{+}}{Z_{0}}}e^{\imath (\omega t-\gamma z)}\left(1-\Gamma e^{\imath (\phi _{z}+2\gamma z)}\right)}
Thus we have
d
2
v
d
L
2
=
γ
2
v
{\displaystyle {\frac {d^{2}v}{dL^{2}}}=\gamma ^{2}v}
γ
2
=
(
R
+
ı
ω
L
)
(
G
+
ı
ω
C
)
{\displaystyle \gamma ^{2}=(R+\imath \omega L)(G+\imath \omega C)}
Z
0
=
v
+
i
+
=
−
v
−
i
−
=
R
′
+
ı
ω
L
′
G
′
+
ı
ω
C
′
{\displaystyle Z_{0}={\frac {v^{+}}{i^{+}}}=-{\frac {v^{-}}{i^{-}}}={\sqrt {\frac {R'+\imath \omega L'}{G'+\imath \omega C'}}}}
For lossless line
R
′
=
G
′
=
0
{\displaystyle R'=G'=0}
R
′
/
L
′
=
G
′
/
C
′
{\displaystyle R'/L'=G'/C'}
Γ
{\displaystyle \Gamma }
Γ
=
v
−
v
+
=
−
i
−
i
+
=
Z
L
−
Z
0
Z
L
+
Z
0
{\displaystyle \Gamma ={\frac {v^{-}}{v^{+}}}=-{\frac {i^{-}}{i^{+}}}={\frac {Z_{L}-Z_{0}}{Z_{L}+Z_{0}}}}
Z
0
{\displaystyle Z_{0}}
Z
L
{\displaystyle Z_{L}}
Z
L
=
Z
0
{\displaystyle Z_{L}=Z_{0}}
perfectly matched , and there is no mismatch loss and all power is transferred to the load (antenna).
An open circuit:
Z
L
=
∞
{\displaystyle Z_{L}=\infty }
Γ
=
+
1
{\displaystyle \Gamma =+1}
A short circuit:
Z
L
=
0
{\displaystyle Z_{L}=0}
Γ
=
−
1
{\displaystyle \Gamma =-1}
A matched load:
Z
L
=
Z
0
{\displaystyle Z_{L}=Z_{0}}
Γ
=
0
{\displaystyle \Gamma =0}
The voltage standing wave ratio or VSWR
VSWR
=
|
V
|
max
|
|
V
|
min
|
=
1
+
|
Γ
|
1
−
|
Γ
|
{\displaystyle {\text{VSWR}}={\frac {|V|_{\text{max}}}{||V|_{\text{min}}|}}={\frac {1+|\Gamma |}{1-|\Gamma |}}}
https://electronics.stackexchange.com/questions/543100/derivation-of-resistance-of-coaxial-cable . Koaksaalikaapelin εr
76.7 Ω
30 Ω
The impedance of a centre-fed dipole antenna in free space is 73 Ω, so 75 Ω coax is commonly used for connecting shortwave antennas to receivers.
Sometimes 300 Ω folded dipole antenna => 4:1 balun transformer is used. twin-lead transmission lines: the characteristic impedance of is roughly 300 Ω.
Feeding length.
Some transmission lines are
Coaxial cable
Two-wire cable
Microstrip line
. . . Skin Effect The skin effect
δ
{\displaystyle \delta }
Balun Velocity factor
Caption text
Velocity factor
Line type
0.95
Ladder line
0.82
Twin-lead
0.79
coaxial cable (foam dielectric)
0.75
RG-6 and RG-8 coaxial (thick)
0.66
RG-58 and RG-59 coaxial (thin)
Something else References 
