High frequency transmission lines

Teoriaa: Systeemi

Error creating thumbnail: convert-im6.q16: unrecognized color `context-fill' @ warning/color.c/GetColorCompliance/1057. convert-im6.q16: non-conforming drawing primitive definition `fill' @ error/draw.c/RenderMVGContent/4414.

Dipole antennas and transmission coefficient. See the svg file

Antenn system.

Lähetin, johto, antenni, jne. https://www.antenna-theory.com/tutorial/txline/transmissionline.php

https://www.worldradiohistory.com/BOOKSHELF-ARH/Technology/Rider-Books/R-F%20Transmission%20Lines%20-%20Alexander%20Schure.pdf

Transmission line

• 

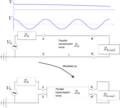
  The (long) transmission line is modeled as $Z_{0}$. If the frequency (wavelength) of the source is too large (small) compared to dimensions of the system, it need to be considered in more detailed. See also the svg file.

• 

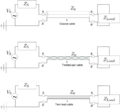
  The physical realizations of the transmission lines are usually coaxial cables, twisted cables or twin lead cables.

• 

  The system is analyzed as being differential short pieces. The conductance Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle G} is the conductance between the two wires, which exists because of the high frequency.

Transmission line

• Coaxial cable
• Two-wire cable
• Microstrip line
• . . .

If a transmission line has a length greater than about 10% of a wavelength, then the line length will noticeably affect the circuit's impedance. The solutions to the above equations is the sum of forward and backward traveling (reflected) waves: $v(z,t)=v^{+}e^{-\alpha z}e^{\imath (\omega t-\gamma z)}+v^{-}e^{\alpha z}e^{\imath (\omega t+\gamma z)}$ and if we assume that Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \alpha =0} we have the telegraphers equations https://en.wikipedia.org/wiki/Telegrapher's_equations

$v(z,t)=v^{+}e^{\imath (\omega t-\gamma z)}+v^{-}e^{\imath (\omega t+\gamma z)}$ and a similar for Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle i=i(z,t)} . If we replace $i$ by Ohm law, we get

$i(z,t)={\frac {v^{+}}{Z_{0}}}e^{\imath (\omega t-\gamma z)}+{\frac {v^{-}}{Z_{0}}}e^{\imath (\omega t+\gamma z)}={\frac {v^{+}}{Z_{0}}}e^{\imath (\omega t-\gamma z)}\left(1-{\frac {v^{-}}{v^{+}}}e^{\imath (2\gamma z)}\right)$

The fraction ${\frac {v^{-}}{v^{+}}}$ is called reflection coefficient $\Gamma$

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{v^-}{v^+} = \Gamma e^{\imath \phi_z} = \frac{Z_L - Z_0}{Z_L + Z_0}}

which gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i(z,t) = = \frac{v^+}{Z_0} e^{\imath (\omega t - \gamma z)} \left( 1 - \Gamma e^{\imath(\phi_z +2\gamma z)} \right) }

The characteristic impedance is

Thus we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2 v}{dL^2} = \gamma^2 v } and similar for the current. The constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma^2 = (R+\imath \omega L)(G+\imath \omega C)} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_0 = \frac{v^+}{i^+} = - \frac{v^-}{i^-} = \sqrt{ \frac{R' + \imath \omega L'}{G' + \imath \omega C'}} }

For lossless line Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R' = G' = 0} and for distortionless line Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R'/L' = G'/C'} . The voltage reflection coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = \frac{v^-}{v^+} = - \frac{i^-}{i^+} = \frac{Z_L - Z_0}{Z_L + Z_0} } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_0} is the characteristic impedance of transient line, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L} is the impedance of load (antenna). If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L= Z_0} , then the line is perfectly matched, and there is no mismatch loss and all power is transferred to the load (antenna).

• An open circuit: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L = \infty} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = +1} .
• A short circuit: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L = 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = -1} , and a phase reversal of the reflected voltage wave.
• A matched load: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L = Z_0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = 0} and no reflections.

The voltage standing wave ratio or VSWR

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{VSWR} = \frac{|V|_\text{max}}{||V|_\text{min}|} = \frac{1 + |\Gamma|}{1 - |\Gamma|} }

Siirtolinja (transmission line). Impedanssi. Koaksaalikaapelin impedanssi muodostuu sen kapasitiivisestä rakenteesta. Ei juuri resistiivistä häviötä (impedanssia) https://electronics.stackexchange.com/questions/543100/derivation-of-resistance-of-coaxial-cable. Koaksaalikaapelin ε^r

• 76.7 Ω
• 30 Ω
• The impedance of a centre-fed dipole antenna in free space is 73 Ω, so 75 Ω coax is commonly used for connecting shortwave antennas to receivers.
• Sometimes 300 Ω folded dipole antenna => 4:1 balun transformer is used.

twin-lead transmission lines: the characteristic impedance of is roughly 300 Ω.

Feeding length.

Skin Effect

The skin effect Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} . The higher the frequency, the more the currents are confined to the surface.

Velocity factor

Caption text

Velocity factor	Line type
0.95	Ladder line
0.82	Twin-lead
0.79	coaxial cable (foam dielectric)
0.75	RG-6 and RG-8 coaxial (thick)
0.66	RG-58 and RG-59 coaxial (thin)