Line 64:
Line 64: \begin{align}
\begin{align}
y_0 &= (1-x^2)^{0/2}
y_0 &= (1-x^2)^{0/2}
= (1-x^2)^0 = 1
= (1-x^2)^0 = 1 =
&&\to && A(y_0) = x
&&\to && A(y_0) = x = \frac11 x
\\
\\
y_1 &= (1-x^2)^{1/2}
y_1 &= (1-x^2)^{1/2}
Line 71:
Line 71: y_2 &= (1-x^2)^{2/2}
y_2 &= (1-x^2)^{2/2}
= 1-x^2
= 1-x^2
&&\to && A(y_2) = x - \frac13 x^3
&&\to && A(y_2) = x - \frac13 x^3 = \frac11 x - \frac13 x^3
\\
\\
y_3 &= (1-x^2)^{3/2}
y_3 &= (1-x^2)^{3/2}
Line 77:
Line 77: y_4 &= (1-x^2)^{4/2}
y_4 &= (1-x^2)^{4/2}
= (1-x^2)^2 = 1 - 2x^2 + x^4
= (1-x^2)^2 = 1 - 2x^2 + x^4
&&\to && A(y_4) = x - \frac23 x^3 + \frac15 x^5
&&\to && A(y_4) = x - \frac23 x^3 + \frac15 x^5 = \frac11 x - \frac23 x^3 + \frac15 x^5
\\
\\
y_5 &= (1-x^2)^{5/2}
y_5 &= (1-x^2)^{5/2}
Line 84:
Line 84: = (1-x^2)^3 = 1 - 3x^2 + 3x^4 -x^6
= (1-x^2)^3 = 1 - 3x^2 + 3x^4 -x^6
&&\to && A(y_6) = x - x^3 + \frac35 x^5 - \frac17x^7
&&\to && A(y_6) = x - x^3 + \frac35 x^5 - \frac17x^7
= x - \frac33 x^3 + \frac35 x^5 - \frac17x^7
= \frac11 x - \frac33 x^3 + \frac35 x^5 - \frac17x^7
\end{align}
\end{align}
</math>
</math>
Revision as of 20:14, 19 October 2022
Introduction Binomial expansion
(
a
+
b
)
0
=
1
(
a
+
b
)
1
=
a
+
b
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
(
a
+
b
)
3
=
(
a
+
b
)
(
a
+
b
)
2
=
(
a
+
b
)
(
a
2
+
2
a
b
+
b
2
)
=
a
3
+
2
a
2
b
+
a
b
2
+
b
a
2
+
2
a
b
2
+
b
3
=
a
3
+
3
a
2
b
+
3
a
b
2
+
b
3
(
a
+
b
)
4
=
⋯
{\displaystyle {\begin{aligned}(a+b)^{0}&=1\\(a+b)^{1}&=a+b\\(a+b)^{2}&=a^{2}+2ab+b^{2}\\(a+b)^{3}&=(a+b)(a+b)^{2}=(a+b)(a^{2}+2ab+b^{2})\\&=a^{3}+2a^{2}b+ab^{2}+ba^{2}+2ab^{2}+b^{3}\\&=a^{3}+3a^{2}b+3ab^{2}+b^{3}\\(a+b)^{4}&=\cdots \end{aligned}}}
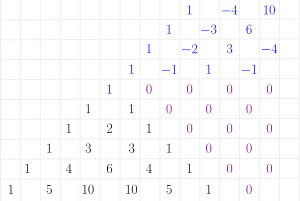
Pascal's triangle Pascal's Triangle The coefficients of binomial expansion can be easily seen from the Pascal triangle. The number is a sum of the two numbers above it.
Pascal's triangle: Negative right This can be extended to negative numbers easily.
Pascal triangle extended to negative values Now, instead of expanding
(
a
+
b
)
n
{\displaystyle (a+b)^{n}}
(
1
+
x
)
n
{\displaystyle (1+x)^{n}}
n
{\displaystyle n}
(
1
+
x
)
−
1
=
1
−
x
+
x
2
−
x
3
+
⋯
(
1
+
x
)
−
2
=
1
−
2
x
+
3
x
2
−
4
x
3
+
⋯
(
1
+
x
)
−
3
=
1
−
3
x
+
6
x
2
−
⋯
{\displaystyle {\begin{aligned}(1+x)^{-1}&=1-x+x^{2}-x^{3}+\cdots \\(1+x)^{-2}&=1-2x+3x^{2}-4x^{3}+\cdots \\(1+x)^{-3}&=1-3x+6x^{2}-\cdots \end{aligned}}}
And by Taylor series (expansion at
x
=
−
1
{\displaystyle x=-1}
Pascal's triangle: Negative left The triangle can be extended to the left also, but it is symmetric to the earlier.
Pascal's triangle: half-integers Newton: Find the area of the curve
y
=
1
−
x
2
=
(
1
−
x
2
)
1
/
2
{\displaystyle y={\sqrt {1-x^{2}}}=(1-x^{2})^{1/2}}
A
=
π
4
{\displaystyle A={\frac {\pi }{4}}}
Wallis and Fermat method that was known:
y
0
=
(
1
−
x
2
)
0
/
2
=
(
1
−
x
2
)
0
=
1
=
→
A
(
y
0
)
=
x
=
1
1
x
y
1
=
(
1
−
x
2
)
1
/
2
y
2
=
(
1
−
x
2
)
2
/
2
=
1
−
x
2
→
A
(
y
2
)
=
x
−
1
3
x
3
=
1
1
x
−
1
3
x
3
y
3
=
(
1
−
x
2
)
3
/
2
y
4
=
(
1
−
x
2
)
4
/
2
=
(
1
−
x
2
)
2
=
1
−
2
x
2
+
x
4
→
A
(
y
4
)
=
x
−
2
3
x
3
+
1
5
x
5
=
1
1
x
−
2
3
x
3
+
1
5
x
5
y
5
=
(
1
−
x
2
)
5
/
2
y
6
=
(
1
−
x
2
)
6
/
2
=
(
1
−
x
2
)
3
=
1
−
3
x
2
+
3
x
4
−
x
6
→
A
(
y
6
)
=
x
−
x
3
+
3
5
x
5
−
1
7
x
7
=
1
1
x
−
3
3
x
3
+
3
5
x
5
−
1
7
x
7
{\displaystyle {\begin{aligned}y_{0}&=(1-x^{2})^{0/2}=(1-x^{2})^{0}=1=&&\to &&A(y_{0})=x={\frac {1}{1}}x\\y_{1}&=(1-x^{2})^{1/2}\\y_{2}&=(1-x^{2})^{2/2}=1-x^{2}&&\to &&A(y_{2})=x-{\frac {1}{3}}x^{3}={\frac {1}{1}}x-{\frac {1}{3}}x^{3}\\y_{3}&=(1-x^{2})^{3/2}\\y_{4}&=(1-x^{2})^{4/2}=(1-x^{2})^{2}=1-2x^{2}+x^{4}&&\to &&A(y_{4})=x-{\frac {2}{3}}x^{3}+{\frac {1}{5}}x^{5}={\frac {1}{1}}x-{\frac {2}{3}}x^{3}+{\frac {1}{5}}x^{5}\\y_{5}&=(1-x^{2})^{5/2}\\y_{6}&=(1-x^{2})^{6/2}=(1-x^{2})^{3}=1-3x^{2}+3x^{4}-x^{6}&&\to &&A(y_{6})=x-x^{3}+{\frac {3}{5}}x^{5}-{\frac {1}{7}}x^{7}={\frac {1}{1}}x-{\frac {3}{3}}x^{3}+{\frac {3}{5}}x^{5}-{\frac {1}{7}}x^{7}\end{aligned}}}
Newton noted that
the first term is always
x
{\displaystyle x}
The denominator is always an odd integer
the second term is
0
3
x
3
{\displaystyle {\frac {0}{3}}x^{3}}
1
3
x
3
{\displaystyle {\frac {1}{3}}x^{3}}
2
3
x
3
{\displaystyle {\frac {2}{3}}x^{3}}
3
3
x
3
{\displaystyle {\frac {3}{3}}x^{3}}
1
{\displaystyle 1}
1
/
2
{\displaystyle 1/2}
0
,
1
2
,
1
,
3
2
,
2
,
5
2
,
3
…
{\displaystyle 0,{\frac {1}{2}},1,{\frac {3}{2}},2,{\frac {5}{2}},3\dots }
A
(
y
1
)
=
(
1
−
x
2
)
1
/
2
=
x
−
1
2
3
x
3
+
⋯
A
(
y
3
)
=
(
1
−
x
2
)
3
/
2
=
x
−
1
+
1
2
3
x
3
+
⋯
A
(
y
5
)
=
(
1
−
x
2
)
5
/
2
=
x
−
1
+
2
2
3
x
3
+
⋯
{\displaystyle {\begin{aligned}A(y_{1})&=(1-x^{2})^{1/2}=x-{\frac {\tfrac {1}{2}}{3}}x^{3}+\cdots \\A(y_{3})&=(1-x^{2})^{3/2}=x-{\frac {\tfrac {1+1}{2}}{3}}x^{3}+\cdots \\A(y_{5})&=(1-x^{2})^{5/2}=x-{\frac {\tfrac {1+2}{2}}{3}}x^{3}+\cdots \end{aligned}}}