Pascal's Triangle

Binomial expansion

${\begin{aligned}(a+b)^{0}&=1\\(a+b)^{1}&=a+b\\(a+b)^{2}&=a^{2}+2ab+b^{2}\\(a+b)^{3}&=(a+b)(a+b)^{2}=(a+b)(a^{2}+2ab+b^{2})\\&=a^{3}+2a^{2}b+ab^{2}+ba^{2}+2ab^{2}+b^{3}\\&=a^{3}+3a^{2}b+3ab^{2}+b^{3}\\(a+b)^{4}&=\cdots \end{aligned}}$

Pascal's triangle

Pascal's Triangle

The coefficients of binomial expansion can be easily seen from the Pascal triangle. The number is a sum of the two numbers above it.

Pascal's triangle: Negative right

This can be extended to negative numbers easily.

Pascal triangle extended to negative values

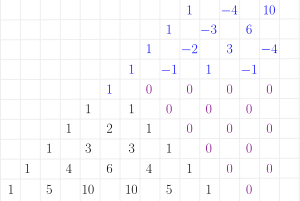
Now, instead of expanding $(a+b)^{n}$, we will use $(1+x)^{n}$, where $n$ is a negative integer. The exponent of each terms grows when going to left. We get according to the Pascal triangle

${\begin{aligned}(1+x)^{-1}&=1-x+x^{2}-x^{3}+\cdots \\(1+x)^{-2}&=1-2x+3x^{2}-4x^{3}+\cdots \\(1+x)^{-3}&=1-3x+6x^{2}-\cdots \end{aligned}}$

And by Taylor series (expansion at $x=-1$Laurent series) we get

• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-1%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-2%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-3%29+%29

Pascal's triangle: Negative left

The triangle can be extended to the left also, but it is symmetric to the earlier.

Pascal's triangle: half-integers

Newton: Find the area of the curve $y={\sqrt {1-x^{2}}}=(1-x^{2})^{1/2}$, because it is a quarter of a unit circle $A={\frac {\pi }{4}}$. He couldn't do that, so he took some other powers, and calculated the areas following Wallis and Fermat method that was known:

${\begin{aligned}y_{0}&=(1-x^{2})^{0/2}=(1-x^{2})^{0}=1&&\to &&A(y_{0})=x\\y_{1}&=(1-x^{2})^{1/2}\\y_{2}&=(1-x^{2})^{2/2}=1-x^{2}&&\to &&A(y_{2})=x-{\frac {1}{3}}x^{3}\\y_{3}&=(1-x^{2})^{3/2}\\y_{4}&=(1-x^{2})^{4/2}=(1-x^{2})^{2}=1-2x^{2}+x^{4}&&\to &&A(y_{4})=x-{\frac {2}{3}}x^{3}+{\frac {1}{5}}x^{5}\\y_{5}&=(1-x^{2})^{5/2}\\y_{6}&=(1-x^{2})^{6/2}=(1-x^{2})^{3}=1-3x^{2}+3x^{4}-x^{6}&&\to &&A(y_{6})=x-x^{3}+{\frac {3}{5}}x^{5}-{\frac {1}{7}}x^{7}\end{aligned}}$

Newton noted that

• the first term is always $x$
• The denominator is always an odd integer
• the second term is ${\frac {0}{3}}x^{3}$, ${\frac {1}{3}}x^{3}$, ${\frac {2}{3}}x^{3}$, ${\frac {3}{3}}x^{3}$, etc.
• Thus, because the numerator of the second term is separated by $1$ he assumed that when adding the half-integers into the list, the separation will be $1/2$, also $0,{\frac {1}{2}},1,{\frac {3}{2}},2,{\frac {5}{2}},3\dots$

So, this will give the the first and second term half-integer to be

${\begin{aligned}A(y_{1})&=(1-x^{2})^{1/2}=x-{\frac {1}{3}}\left({\frac {1}{2}}x^{2}\right)+\cdots \\A(y_{3})&=(1-x^{2})^{3/2}=x-{\frac {1}{3}}\left({\frac {2}{3}}x^{2}\right)+\cdots \\A(y_{5})&=(1-x^{2})^{5/2}=x-{\frac {1}{3}}\left({\frac {5}{2}}x^{2}\right)+\cdots \end{aligned}}$