Quantum Gates

Introduction

Import the modules

from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector

Plot the quantum circuit </syntaxhighlight> qc.draw('mpl') </syntaxhighlight>

Plot the results

backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
qc.measure_all()
qc.draw()
result = execute(qc,backend).result()
counts = result.get_counts()
plot_histogram(counts)

Quantum Gates of One Qubit

There are only two reversible gates, also identity (return the input unchanged) and NOT (return the opposite of the input), but neither is universal.

Identity gate.

Pauli X gate. $\sigma _{x}=X={\begin{bmatrix}0&1\\1&0\end{bmatrix}}=|0\rangle \langle 1|+|1\rangle \langle 0|$

Pauli Y gate $\sigma _{y}=Y={\begin{bmatrix}0&-i\\i&0\end{bmatrix}}=-i|0\rangle \langle 1|+i|1\rangle \langle 0|$

Pauli Z gate $\sigma _{z}=Z={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}=|0\rangle \langle 0|-|1\rangle \langle 1|$

Hadamard gate $H={\tfrac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}=|+\rangle \langle 0|+|-\rangle \langle 1|$

R gate $R_{\phi }={\begin{bmatrix}1&0\\0&e^{i\phi }\end{bmatrix}}$

S gate or ${\sqrt {Z}}$ gate $S={\begin{bmatrix}1&0\\0&e^{\frac {i\pi }{2}}\end{bmatrix}}$

T gate $T={\begin{bmatrix}1&0\\0&e^{\frac {i\pi }{4}}\end{bmatrix}}$

U1 gate: $U_{1}=U_{3}(0,0,\lambda )=U_{1}={\begin{bmatrix}1&0\\0&e^{i\lambda }\\\end{bmatrix}}$

U2 gate: $U_{2}=U_{3}({\tfrac {\pi }{2}},\phi ,\lambda )={\tfrac {1}{\sqrt {2}}}{\begin{bmatrix}1&-e^{i\lambda }\\e^{i\phi }&e^{i\lambda +i\phi }\end{bmatrix}}$

qc = QuantumCircuit(1)
qc.x(0)
#qc.y(0) # Y-gate on qubit 0
#qc.z(0) # Z-gate on qubit 0
#qc.rz(pi/4, 0)
#qc.s(0)   # Apply S-gate to qubit 0
#qc.sdg(0) # Apply Sdg-gate to qubit 0
qc.t(0)   # Apply T-gate to qubit 0
qc.tdg(0) # Apply Tdg-gate to qubit 0

qc.draw('mpl')
# Let's see the result
backend = Aer.get_backend('statevector_simulator')
out = execute(qc,backend).result().get_statevector()
plot_bloch_multivector(out)

Two Qubit Quantum Gates

The reversibel gates are eg. identity, or CNOT.

Eg. $X\otimes H={\begin{bmatrix}0&H\\H&0\end{bmatrix}}$.

backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,backend).result().get_unitary()
#
# In Jupyter Notebooks we can display this nicely using Latex.
# If not using Jupyter Notebooks you may need to remove the 
# array_to_latex function and use print(unitary) instead.
from qiskit_textbook.tools import array_to_latex
array_to_latex(unitary, pretext="\\text{Circuit = }\n")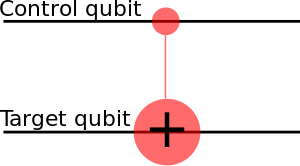

CNOT gate as a pictoram.

Eg. CNOT is a conditional gate that performs an X-gate on the second qubit, if the state of the first qubit (control) is $|1\rangle$. $CNOT={\begin{bmatrix}1&0&0&0\\0&0&0&1\\0&0&1&0\\0&1&0&0\\\end{bmatrix}}$. This matrix swaps the amplitudes of |01⟩ and |11⟩ in the statevector. ${\text{CNOT}}(x,y)=(x,x\otimes y)$.

CNOT if a control qubit is on the superposition:

${\text{CNOT}}|{-}0\rangle =|{-}0\rangle$

${\text{CNOT}}|{-}1\rangle =-|{-}1\rangle$

${\text{CNOT}}|0{+}\rangle ={\tfrac {1}{\sqrt {2}}}(|00\rangle +|11\rangle )$, which is Bell State. Entanglement, but no-communication theorem.

${\text{CNOT}}|{+}{+}\rangle =|{+}{+}\rangle )$. Unchanged.

${\text{CNOT}}|{-}{+}\rangle ={\tfrac {1}{\sqrt {2}}}(|{-}0\rangle -|{-}1\rangle )=|{-}{-}\rangle$

${\text{CNOT}}|{+}{-}\rangle =$.

${\text{CNOT}}|{-}{-}\rangle ={\tfrac {1}{2}}(|00\rangle -|01\rangle -|10\rangle +|11\rangle )=|{-}{-}\rangle$. Affects the state of the control qubit, only.

qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
# Apply a CNOT:
qc.cx(0,1)
qc.draw('mpl')
#
# Let's see the result:
backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc,backend).result().get_statevector()
# Print the statevector neatly:
array_to_latex(final_state, pretext="\\text{Statevector = }")
#
results = execute(qc,backend).result().get_counts()
plot_histogram(results)

Any controlled quantum gate is ${\text{Controlled-U}}={\begin{bmatrix}I&0\\0&U\end{bmatrix}}$ and in Qiskit formalism is written in matrix as ${\text{Controlled-U}}={\begin{bmatrix}1&0&0&0\\0&u_{00}&0&u_{01}\\0&0&1&0\\0&u_{10}&0&u_{11}\\\end{bmatrix}}$

Controlled-Z. Because $HXH=Z$ and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H Z H = X} we can write

qc = QuantumCircuit(2)
# also a controlled-Z
qc.h(t)
qc.cx(c,t)
qc.h(t)
qc.draw('mpl')

Controlled-Y is

qc = QuantumCircuit(2)
# a controlled-Y
qc.sdg(t)
qc.cx(c,t)
qc.s(t)
qc.draw('mpl')

or Controlled-H is

qc = QuantumCircuit(2)
# a controlled-H
qc.ry(pi/4,t)
qc.cx(c,t)
qc.ry(-pi/4,t)
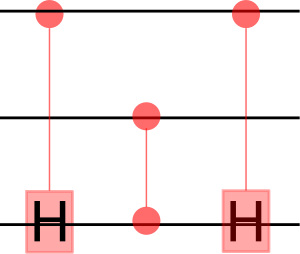
qc.draw('mpl')

Swap gate

An arbitrary controlled-controlled-U for any single-qubit rotation U. We need Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \sqrt U} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V^\dagger}

#The controls are qubits a and b, and the target is qubit t.
#Subroutines cu1(theta,c,t) and cu1(-theta,c,t) need to be defined
qc = QuantumCircuit(3)
qc.cu1(theta,b,t)
qc.cx(a,b)
qc.cu1(-theta,b,t)
qc.cx(a,b)
qc.cu1(theta,a,t)
qc.draw('mpl')

Three Qubits

Toffoli gate made using CNOTs.

For universal computations we need more qubits. Eg. the AND gate is not reversible, and thus we need eg. Toffoli (CCNOT) gate.

Toffoli gate performs Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} on target qubit if both control cubits are set to state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1\rangle} .

qc = QuantumCircuit(3)
a = 0
b = 1
t = 2
# Toffoli with control qubits a and b and target t
qc.ccx(a,b,t)
qc.draw()

Toffoli using CNOTs uses fewer gates.

qc = QuantumCircuit(3)
qc.ch(a,t)
qc.cz(b,t)
qc.ch(a,t)
qc.draw()

AND gate is Toffoli gate with . . .

The nand gate

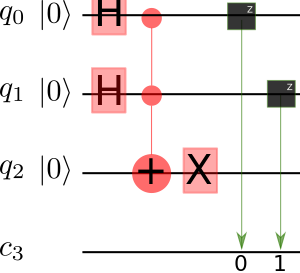
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{CCNOT}(x,y,z) = (x,y,( x \and y ) \otimes z )} gives the reversible NAND Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{NAND}(x,y) = \text{CCNOT}(x,y,1) = (x,y,( x \and y ) \otimes 1 )}

NAND gate is