Pascal's Triangle: Difference between revisions
| Line 65: | Line 65: | ||
y_0 &= (1-x^2)^{0/2} | y_0 &= (1-x^2)^{0/2} | ||
= (1-x^2)^0 = 1 = | = (1-x^2)^0 = 1 = | ||
&&\to && A(y_0) = x | &&\to && A(y_0) = x = \frac11 x | ||
\\ | \\ | ||
y_1 &= (1-x^2)^{1/2} | y_1 &= (1-x^2)^{1/2} | ||
| Line 71: | Line 71: | ||
y_2 &= (1-x^2)^{2/2} | y_2 &= (1-x^2)^{2/2} | ||
= 1-x^2 | = 1-x^2 | ||
&&\to && A(y_2) = x - \frac13 x^3 | &&\to && A(y_2) = x - \frac13 x^3 = \frac11 x - \frac13 x^3 | ||
\\ | \\ | ||
y_3 &= (1-x^2)^{3/2} | y_3 &= (1-x^2)^{3/2} | ||
| Line 78: | Line 78: | ||
= (1-x^2)^2 = 1 - 2x^2 + x^4 | = (1-x^2)^2 = 1 - 2x^2 + x^4 | ||
&&\to && A(y_4) | &&\to && A(y_4) | ||
= x - \frac23 x^3 + \frac15 x^5 = \frac11 x - \frac23 x^3 + \frac15 x^5 | |||
\\ | \\ | ||
y_5 &= (1-x^2)^{5/2} | y_5 &= (1-x^2)^{5/2} | ||
| Line 85: | Line 85: | ||
= (1-x^2)^3 = 1 - 3x^2 + 3x^4 -x^6 | = (1-x^2)^3 = 1 - 3x^2 + 3x^4 -x^6 | ||
&&\to && A(y_6) = x - x^3 + \frac35 x^5 - \frac17x^7 | &&\to && A(y_6) = x - x^3 + \frac35 x^5 - \frac17x^7 | ||
= \frac11 x - \frac33 x^3 + \frac35 x^5 - \frac17x^7 | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
Revision as of 20:16, 19 October 2022
Introduction
Binomial expansion
Pascal's triangle

The coefficients of binomial expansion can be easily seen from the Pascal triangle. The number is a sum of the two numbers above it.
Pascal's triangle: Negative right
This can be extended to negative numbers easily.
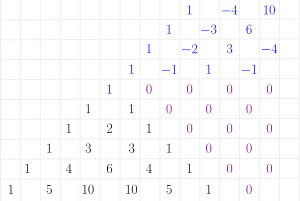
Now, instead of expanding , we will use , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is a negative integer. The exponent of each terms grows when going to left. We get according to the Pascal triangle
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (1+x)^{-1} &= 1 - x + x^2 - x^3 + \cdots \\ (1+x)^{-2} &= 1 - 2x + 3x^2 - 4x^3 + \cdots \\ (1+x)^{-3} &= 1 - 3x + 6x^2 - \cdots \end{align} }
And by Taylor series (expansion at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=-1} Laurent series) we get
- https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-1%29+%29
- https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-2%29+%29
- https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-3%29+%29
Pascal's triangle: Negative left
The triangle can be extended to the left also, but it is symmetric to the earlier.
Pascal's triangle: half-integers
Newton: Find the area of the curve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = \sqrt{1-x^2}=(1-x^2)^{1/2}} , because it is a quarter of a unit circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A= \frac\pi 4} . He couldn't do that, so he took some other powers, and calculated the areas following Wallis and Fermat method that was known:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} y_0 &= (1-x^2)^{0/2} = (1-x^2)^0 = 1 = &&\to && A(y_0) = x = \frac11 x \\ y_1 &= (1-x^2)^{1/2} \\ y_2 &= (1-x^2)^{2/2} = 1-x^2 &&\to && A(y_2) = x - \frac13 x^3 = \frac11 x - \frac13 x^3 \\ y_3 &= (1-x^2)^{3/2} \\ y_4 &= (1-x^2)^{4/2} = (1-x^2)^2 = 1 - 2x^2 + x^4 &&\to && A(y_4) = x - \frac23 x^3 + \frac15 x^5 = \frac11 x - \frac23 x^3 + \frac15 x^5 \\ y_5 &= (1-x^2)^{5/2} \\ y_6 &= (1-x^2)^{6/2} = (1-x^2)^3 = 1 - 3x^2 + 3x^4 -x^6 &&\to && A(y_6) = x - x^3 + \frac35 x^5 - \frac17x^7 = \frac11 x - \frac33 x^3 + \frac35 x^5 - \frac17x^7 \end{align} }
Newton noted that
- the first term is always Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . He assumed that that is true also for half-integer numbers
- The denominator is always an odd integer
- the second term is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac03 x^3} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac13 x^3} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac23 x^3} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac33 x^3} , etc. Thus, because the numerator of the second term is separated by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} he assumed that when adding the half-integers into the list, the separation will be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2} , also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0, \frac12, 1, \frac 32, 2, \frac52, 3\dots} . So, this will give the the first and second term half-integer to be
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} A(y_1) &= (1-x^2)^{1/2} = x - \frac {\tfrac12}3 x^3 + \cdots \\ A(y_3) &= (1-x^2)^{3/2} = x - \frac {\tfrac{1+1}2}3 x^3 + \cdots \\ A(y_5) &= (1-x^2)^{5/2} = x - \frac {\tfrac{1+2}2}3 x^3 + \cdots \end{align} }


