Pascal's Triangle

Binomial expansion

${\begin{aligned}(a+b)^{0}&=1\\(a+b)^{1}&=a+b\\(a+b)^{2}&=a^{2}+2ab+b^{2}\\(a+b)^{3}&=(a+b)(a+b)^{2}=(a+b)(a^{2}+2ab+b^{2})\\&=a^{3}+2a^{2}b+ab^{2}+ba^{2}+2ab^{2}+b^{3}\\&=a^{3}+3a^{2}b+3ab^{2}+b^{3}\\(a+b)^{4}&=\cdots \end{aligned}}$

Pascal's triangle

Pascal's Triangle

The coefficients of binomial expansion can be easily seen from the Pascal triangle. The number is a sum of the two numbers above it.

Pascal's triangle: Negative right

This can be extended to negative numbers easily.

Pascal triangle extended to negative values

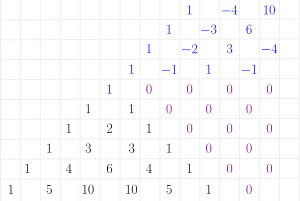
Now, instead of expanding Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a+b)^n} , we will use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1+x)^n} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is a negative integer. The exponent of each terms grows when going to left. We get according to the Pascal triangle

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (1+x)^{-1} &= 1 - x + x^2 - x^3 + \cdots \\ (1+x)^{-2} &= 1 - 2x + 3x^2 - 4x^3 + \cdots \\ (1+x)^{-3} &= 1 - 3x + 6x^2 - \cdots \end{align} }

And by Taylor series (expansion at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=-1} Laurent series) we get

• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-1%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-2%29+%29
• https://www.wolframalpha.com/input?i=series%28+%281%2Bx%29%5E%28-3%29+%29

Pascal's triangle: Negative left

The triangle can be extended to the left also, but it is symmetric to the earlier.

Pascal's triangle: half-integers

Newton: Find the area of the curve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = \sqrt{1-x^2}=(1-x^2)^{1/2}} , because it is a quarter of a unit circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A= \frac\pi 4} . He couldn't do that, so he took some other powers, and calculated the areas following Wallis and Fermat method that was known:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} y_0 &= (1-x^2)^{0/2} = (1-x^2)^0 = 1 &&\to && A(y_0) = x \\ y_1 &= (1-x^2)^{1/2} \\ y_2 &= (1-x^2)^{2/2} = 1-x^2 &&\to && A(y_2) = x - \frac13 x^3 \\ y_3 &= (1-x^2)^{3/2} \\ y_4 &= (1-x^2)^{4/2} = (1-x^2)^2 = 1 - 2x^2 + x^4 &&\to && A(y_4) = x - \frac23 x^3 + \frac15 x^5 \\ y_5 &= (1-x^2)^{5/2} \\ y_6 &= (1-x^2)^{6/2} = (1-x^2)^3 = 1 - 3x^2 + 3x^4 -x^6 &&\to && A(y_6) = x - x^3 + \frac35 x^5 - \frac17x^7 \end{align} }

Newton noted that

• the first term is always Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
• The denominator is always an odd integer
• the second term is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac03 x^3} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac13 x^3} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac23 x^3} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac33 x^3} , etc.
• Thus, because the numerator of the second term is separated by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} he assumed that when adding the half-integers into the list, the separation will be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2} , also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0, \frac12, 1, \frac 32, \dots}

So, this will give the the first and second term half-integer to be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} y_1 &= (1-x^2)^{1/2} = x - \frac 13 \left( \frac12 x^2 \right) + \cdots \\ y_3 &= (1-x^2)^{3/2} = x - \frac 13 \left( \frac32 x^2 \right) + \cdots \\ y_5 &= (1-x^2)^{5/2} = x - \frac 13 \left( \frac52 x^2 \right) + \cdots \end{align} }