Pascal's Triangle

Binomial expansion

${\begin{aligned}(a+b)^{0}&=1\\(a+b)^{1}&=a+b\\(a+b)^{2}&=a^{2}+2ab+b^{2}\\(a+b)^{3}&=(a+b)(a+b)^{2}=(a+b)(a^{2}+2ab+b^{2})\\&=a^{3}+2a^{2}b+ab^{2}+ba^{2}+2ab^{2}+b^{3}\\&=a^{3}+3a^{2}b+3ab^{2}+b^{3}\\(a+b)^{4}&=\cdots \end{aligned}}$

Pascal's triangle

Pascal's Triangle

The coefficients of binomial expansion can be easily seen from the Pascal triangle. The number is a sum of the two numbers above it.

Pascal's triangle: Negative 1

This can be extended to negative numbers easily.

Pascal triangle extended to negative values

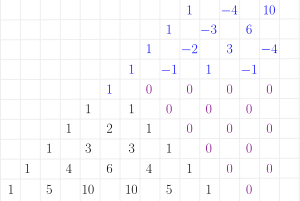
Now, instead of expanding $(a+b)^{n}$, we will use $(1+x)^{n}$, where $n$ is a negative integer. The exponent of each terms grows when going to left. We get according to the Pascal triangle

${\begin{aligned}(1+x)^{-1}&=1-x+x^{2}-x^{3}+\cdots \\(1+x)^{-2}&=1-2x+3x^{2}-4x^{3}+\cdots \\(1+x)^{-3}&=1-3x+6x^{2}-\cdots \end{aligned}}$