Line 74:
Line 74: Eg. <math>X\otimes H = \begin{bmatrix} 0 &H\\H&0\end{bmatrix}</math>.
Eg. <math>X\otimes H = \begin{bmatrix} 0 &H\\H&0\end{bmatrix}</math>.
<syntaxhighlight>
backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,backend).result().get_unitary()
</syntaxhighlight>
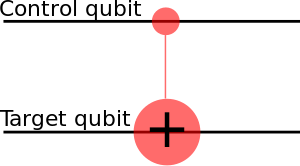
[[File:Cnot.svg|thumb|CNOT gate as a pictoram.]]
[[File:Cnot.svg|thumb|CNOT gate as a pictoram.]]
Line 107:
Line 103: <syntaxhighlight>
<syntaxhighlight>
qc = QuantumCircuit(2)
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0) # Apply H-gate to the first:
qc.h(0)
qc.cx (0,1 ) # Apply a CNOT:
# Apply a CNOT:
qc.cx(0,1)
qc.draw('mpl')
#
# Let's see the result:
backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc,backend).result().get_statevector()
# Print the statevector neatly:
array_to_latex(final_state, pretext="\\text{Statevector = }")
#
results = execute(qc,backend).result().get_counts()
plot_histogram(results)
</syntaxhighlight>
</syntaxhighlight>
Introduction Import the modules
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector Plot the quantum circuit
</syntaxhighlight>
qc.draw('mpl')
</syntaxhighlight>
Plot the results
backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
qc.measure_all()
qc.draw()
result = execute(qc,backend).result()
counts = result.get_counts()
plot_histogram(counts) Quantum Gates of One Qubit There are only two reversible gates, also identity (return the input unchanged) and NOT (return the opposite of the input), but neither is universal.
Identity gate.
Pauli X gate.
σ
x
=
X
=
[
0
1
1
0
]
=
|
0
⟩
⟨
1
|
+
|
1
⟩
⟨
0
|
{\displaystyle \sigma _{x}=X={\begin{bmatrix}0&1\\1&0\end{bmatrix}}=|0\rangle \langle 1|+|1\rangle \langle 0|}
Pauli Y gate
σ
y
=
Y
=
[
0
−
i
i
0
]
=
−
i
|
0
⟩
⟨
1
|
+
i
|
1
⟩
⟨
0
|
{\displaystyle \sigma _{y}=Y={\begin{bmatrix}0&-i\\i&0\end{bmatrix}}=-i|0\rangle \langle 1|+i|1\rangle \langle 0|}
Pauli Z gate
σ
z
=
Z
=
[
1
0
0
−
1
]
=
|
0
⟩
⟨
0
|
−
|
1
⟩
⟨
1
|
{\displaystyle \sigma _{z}=Z={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}=|0\rangle \langle 0|-|1\rangle \langle 1|}
Hadamard gate
H
=
1
2
[
1
1
1
−
1
]
=
|
+
⟩
⟨
0
|
+
|
−
⟩
⟨
1
|
{\displaystyle H={\tfrac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}=|+\rangle \langle 0|+|-\rangle \langle 1|}
R gate
R
ϕ
=
[
1
0
0
e
i
ϕ
]
{\displaystyle R_{\phi }={\begin{bmatrix}1&0\\0&e^{i\phi }\end{bmatrix}}}
S gate or
Z
{\displaystyle {\sqrt {Z}}}
S
=
[
1
0
0
e
i
π
2
]
{\displaystyle S={\begin{bmatrix}1&0\\0&e^{\frac {i\pi }{2}}\end{bmatrix}}}
T gate
T
=
[
1
0
0
e
i
π
4
]
{\displaystyle T={\begin{bmatrix}1&0\\0&e^{\frac {i\pi }{4}}\end{bmatrix}}}
U1 gate:
U
1
=
U
3
(
0
,
0
,
λ
)
=
U
1
=
[
1
0
0
e
i
λ
]
{\displaystyle U_{1}=U_{3}(0,0,\lambda )=U_{1}={\begin{bmatrix}1&0\\0&e^{i\lambda }\\\end{bmatrix}}}
U2 gate:
U
2
=
U
3
(
π
2
,
ϕ
,
λ
)
=
1
2
[
1
−
e
i
λ
e
i
ϕ
e
i
λ
+
i
ϕ
]
{\displaystyle U_{2}=U_{3}({\tfrac {\pi }{2}},\phi ,\lambda )={\tfrac {1}{\sqrt {2}}}{\begin{bmatrix}1&-e^{i\lambda }\\e^{i\phi }&e^{i\lambda +i\phi }\end{bmatrix}}}
qc = QuantumCircuit(1)
qc.x(0)
#qc.y(0) # Y-gate on qubit 0
#qc.z(0) # Z-gate on qubit 0
#qc.rz(pi/4, 0)
#qc.s(0) # Apply S-gate to qubit 0
#qc.sdg(0) # Apply Sdg-gate to qubit 0
qc.t(0) # Apply T-gate to qubit 0
qc.tdg(0) # Apply Tdg-gate to qubit 0 Two Qubit Quantum Gates The reversibel gates are eg. identity , or CNOT.
Eg.
X
⊗
H
=
[
0
H
H
0
]
{\displaystyle X\otimes H={\begin{bmatrix}0&H\\H&0\end{bmatrix}}}
CNOT gate as a pictoram.
|
1
⟩
{\displaystyle |1\rangle }
C
N
O
T
=
[
1
0
0
0
0
0
0
1
0
0
1
0
0
1
0
0
]
{\displaystyle CNOT={\begin{bmatrix}1&0&0&0\\0&0&0&1\\0&0&1&0\\0&1&0&0\\\end{bmatrix}}}
CNOT
(
x
,
y
)
=
(
x
,
x
⊗
y
)
{\displaystyle {\text{CNOT}}(x,y)=(x,x\otimes y)}
CNOT if a control qubit is on the superposition:
CNOT
|
−
0
⟩
=
|
−
0
⟩
{\displaystyle {\text{CNOT}}|{-}0\rangle =|{-}0\rangle }
CNOT
|
−
1
⟩
=
−
|
−
1
⟩
{\displaystyle {\text{CNOT}}|{-}1\rangle =-|{-}1\rangle }
CNOT
|
0
+
⟩
=
1
2
(
|
00
⟩
+
|
11
⟩
)
{\displaystyle {\text{CNOT}}|0{+}\rangle ={\tfrac {1}{\sqrt {2}}}(|00\rangle +|11\rangle )}
Bell State . Entanglement, but no-communication theorem .
CNOT
|
+
+
⟩
=
|
+
+
⟩
)
{\displaystyle {\text{CNOT}}|{+}{+}\rangle =|{+}{+}\rangle )}
CNOT
|
−
+
⟩
=
1
2
(
|
−
0
⟩
−
|
−
1
⟩
)
=
|
−
−
⟩
{\displaystyle {\text{CNOT}}|{-}{+}\rangle ={\tfrac {1}{\sqrt {2}}}(|{-}0\rangle -|{-}1\rangle )=|{-}{-}\rangle }
CNOT
|
+
−
⟩
=
{\displaystyle {\text{CNOT}}|{+}{-}\rangle =}
CNOT
|
−
−
⟩
=
1
2
(
|
00
⟩
−
|
01
⟩
−
|
10
⟩
+
|
11
⟩
)
=
|
−
−
⟩
{\displaystyle {\text{CNOT}}|{-}{-}\rangle ={\tfrac {1}{2}}(|00\rangle -|01\rangle -|10\rangle +|11\rangle )=|{-}{-}\rangle }
qc = QuantumCircuit(2)
qc.h(0) # Apply H-gate to the first:
qc.cx(0,1) # Apply a CNOT:
Any controlled quantum gate is
Controlled-U
=
[
I
0
0
U
]
{\displaystyle {\text{Controlled-U}}={\begin{bmatrix}I&0\\0&U\end{bmatrix}}}
Controlled-U
=
[
1
0
0
0
0
u
00
0
u
01
0
0
1
0
0
u
10
0
u
11
]
{\displaystyle {\text{Controlled-U}}={\begin{bmatrix}1&0&0&0\\0&u_{00}&0&u_{01}\\0&0&1&0\\0&u_{10}&0&u_{11}\\\end{bmatrix}}}
Controlled-Z. Because
H
X
H
=
Z
{\displaystyle HXH=Z}
H
Z
H
=
X
{\displaystyle HZH=X}
qc = QuantumCircuit(2)
# also a controlled-Z
qc.h(t)
qc.cx(c,t)
qc.h(t)
qc.draw('mpl') Controlled-Y is
qc = QuantumCircuit(2)
# a controlled-Y
qc.sdg(t)
qc.cx(c,t)
qc.s(t)
qc.draw('mpl') or Controlled-H is
qc = QuantumCircuit(2)
# a controlled-H
qc.ry(pi/4,t)
qc.cx(c,t)
qc.ry(-pi/4,t)
qc.draw('mpl') Swap gate
An arbitrary controlled-controlled-U for any single-qubit rotation U. We need
V
=
U
{\displaystyle V={\sqrt {U}}}
V
†
{\displaystyle V^{\dagger }}
#The controls are qubits a and b, and the target is qubit t.
#Subroutines cu1(theta,c,t) and cu1(-theta,c,t) need to be defined
qc = QuantumCircuit(3)
qc.cu1(theta,b,t)
qc.cx(a,b)
qc.cu1(-theta,b,t)
qc.cx(a,b)
qc.cu1(theta,a,t)
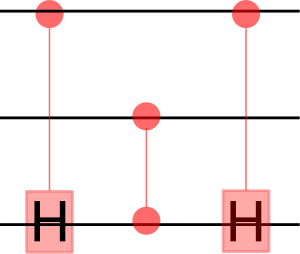
qc.draw('mpl') Three Qubits Toffoli gate made using CNOTs.
Toffoli gate performs
X
{\displaystyle X}
|
1
⟩
{\displaystyle |1\rangle }
qc = QuantumCircuit(3)
a = 0
b = 1
t = 2
# Toffoli with control qubits a and b and target t
qc.ccx(a,b,t)
qc.draw()
qc = QuantumCircuit(3)
qc.ch(a,t)
qc.cz(b,t)
qc.ch(a,t)
qc.draw() AND gate is Toffoli gate with . . .
The nand gate
CCNOT
(
x
,
y
,
z
)
=
(
x
,
y
,
(
x
∧
y
)
⊗
z
)
{\displaystyle {\text{CCNOT}}(x,y,z)=(x,y,(x\land y)\otimes z)}
NAND
(
x
,
y
)
=
CCNOT
(
x
,
y
,
1
)
=
(
x
,
y
,
(
x
∧
y
)
⊗
1
)
{\displaystyle {\text{NAND}}(x,y)={\text{CCNOT}}(x,y,1)=(x,y,(x\land y)\otimes 1)}