High frequency transmission lines: Difference between revisions
(→H) |
|||
| (15 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Antenna system. | |||
Lähetin, johto, antenni, jne. https://www.antenna-theory.com/tutorial/txline/transmissionline.php | Lähetin, johto, antenni, jne. https://www.antenna-theory.com/tutorial/txline/transmissionline.php | ||
https://www.worldradiohistory.com/BOOKSHELF-ARH/Technology/Rider-Books/R-F%20Transmission%20Lines%20-%20Alexander%20Schure.pdf | https://www.worldradiohistory.com/BOOKSHELF-ARH/Technology/Rider-Books/R-F%20Transmission%20Lines%20-%20Alexander%20Schure.pdf | ||
Electrical length instead of physical length. | |||
== Transmission line, general case == | == Transmission line, general case == | ||
=== Images === | |||
<gallery> | <gallery> | ||
| Line 16: | Line 18: | ||
Dipole transmissionLine2.png|thumb|The physical realizations of the transmission lines are usually coaxial cables, twisted cables or twin lead cables. | Dipole transmissionLine2.png|thumb|The physical realizations of the transmission lines are usually coaxial cables, twisted cables or twin lead cables. | ||
Dipole differential transmissionline.png|The system is analyzed as being differential short pieces. The conductance <math>G</math> is the conductance between the two wires, which exists because of the high frequency. | Dipole differential transmissionline.png|The system is analyzed as being differential short pieces. The conductance <math>G</math> is the conductance between the two wires, which exists because of the high frequency. | ||
Dipole differential transmissionline2.png|The characteristic impedance Z<sub>0</sub>. | |||
</gallery> | </gallery> | ||
| Line 36: | Line 39: | ||
</math> | </math> | ||
and similar equation to ''i''. Those are damped, dispersive hyperbolic partial differential equations each involving only one unknown. Lets solve those. | and similar equation to ''i''. Those are damped, dispersive hyperbolic partial differential equations each involving only one unknown. Lets solve those. ([https://en.wikipedia.org/wiki/Telegrapher's_equations Telegrapher's equations]) | ||
=== Lossless transmission === | === Lossless transmission === | ||
| Line 46: | Line 49: | ||
</math> | </math> | ||
where <math> \hat v = (LC)^{-1/2}</math>. These reduce to one-dimensional Helmholtz equations, and the result is | where <math> \hat v = (LC)^{-1/2}</math>. These reduce to one-dimensional Helmholtz equations, or eigenmodes, and the result if an eigenmode is | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
v_\omega(x) &= v^+ e^{-\imath (kx+\omega t)} + v^- e^{+\imath (kx-\omega t)} \\ | |||
i_\omega(x) &= \frac{v^+}{Z_0} e^{-\imath (kx + \omega t)} + \frac{v^-}{Z_0} e^{+\imath (kx-\omega t)} | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Line 60: | Line 63: | ||
Z_0 = \sqrt{ \frac LZ } | Z_0 = \sqrt{ \frac LZ } | ||
</math> | </math> | ||
The full solution can be decomposed into an eigenmode expansion <math>u(x,t) = \int_{-\infty}^\infty s(\omega) v_\omega(x,t) d \omega</math> | |||
=== Lossy transmission line === | === Lossy transmission line === | ||
=== Frequency Domain === | |||
<math> | |||
\begin{align} | |||
\frac{dv_\omega}{d x} &= - (\imath \omega L_\omega + R_\omega) i_\omega(x) \\ | |||
% | |||
\frac{di_\omega}{d x} &= - (\imath \omega C_\omega + G_\omega) v_\omega(x) \\ | |||
\end{align} | |||
</math> | |||
and by combining these we get | |||
<math> | |||
\frac{d^2 v_\omega}{d x^2} = \gamma^2 v_\omega | |||
</math> | |||
and similar for $i$, with <math>\gamma = \alpha + \imath b | |||
= \sqrt{(R_\omega + \imath \omega L_\omega)(G_\omega + \imath \omega C_\omega)}</math> | |||
=== Line termination === | |||
Impedance match | |||
=== Reflections === | |||
=== Standing Waves === | |||
=== Standing Wave Ratio SWR === | |||
The standing wave ratio is a measure of the mismatch of the line termination. | |||
=== S === | === S === | ||
The solutions to the above equations is the sum of forward and backward traveling (reflected) waves: | The solutions to the above equations is the sum of forward and backward traveling (reflected) waves: | ||
Latest revision as of 17:09, 25 August 2025
Introduction
Antenna system.
Lähetin, johto, antenni, jne. https://www.antenna-theory.com/tutorial/txline/transmissionline.php
Electrical length instead of physical length.
Transmission line, general case
Images
-
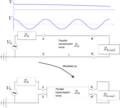
The (long) transmission line is modeled as Z0. If the frequency (wavelength) of the source is too large (small) compared to dimensions of the system, it need to be considered in more detailed. See also the svg file.
-
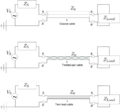
The physical realizations of the transmission lines are usually coaxial cables, twisted cables or twin lead cables.
-
The system is analyzed as being differential short pieces. The conductance is the conductance between the two wires, which exists because of the high frequency.
-
The characteristic impedance Z0.
General case
If a transmission line has a length greater than about 10% of a wavelength, then the line length will noticeably affect the circuit's impedance. The equation in the above image can be written as
and these two is easy to combine, and it gives the second degree dy
and similar equation to i. Those are damped, dispersive hyperbolic partial differential equations each involving only one unknown. Lets solve those. (Telegrapher's equations)
Lossless transmission
If wire resistance and insulation conductance can be neglected (R=G=0), the model depends only on L and C elements. Thus, we have two similar wave equations for v and i (only for v is shown)
where . These reduce to one-dimensional Helmholtz equations, or eigenmodes, and the result if an eigenmode is
where k is the wave number and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_0} is the characteristic impedance, which for the lossles transmission line is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_0 = \sqrt{ \frac LZ } }
The full solution can be decomposed into an eigenmode expansion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(x,t) = \int_{-\infty}^\infty s(\omega) v_\omega(x,t) d \omega}
Lossy transmission line
Frequency Domain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dv_\omega}{d x} &= - (\imath \omega L_\omega + R_\omega) i_\omega(x) \\ % \frac{di_\omega}{d x} &= - (\imath \omega C_\omega + G_\omega) v_\omega(x) \\ \end{align} }
and by combining these we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2 v_\omega}{d x^2} = \gamma^2 v_\omega }
and similar for $i$, with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = \alpha + \imath b = \sqrt{(R_\omega + \imath \omega L_\omega)(G_\omega + \imath \omega C_\omega)}}
Line termination
Impedance match
Reflections
Standing Waves
Standing Wave Ratio SWR
The standing wave ratio is a measure of the mismatch of the line termination.
S
The solutions to the above equations is the sum of forward and backward traveling (reflected) waves: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(z,t) = v^+ e^{-\alpha z} e^{\imath( \omega t - \gamma z )} + v^- e^{\alpha z} e^{\imath (\omega t +\gamma z) } } and if we assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=0} we have the telegraphers equations https://en.wikipedia.org/wiki/Telegrapher's_equations
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(z,t) = v^+ e^{\imath (\omega t - \gamma z)} + v^- e^{\imath (\omega t +\gamma z)} } and a similar for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=i(z,t)} . If we replace $i$ by Ohm law, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i(z,t) = \frac{v^+}{Z_0} e^{\imath (\omega t - \gamma z) } + \frac{v^-}{Z_0} e^{\imath (\omega t +\gamma z)} = \frac{v^+}{Z_0} e^{\imath (\omega t - \gamma z)} \left( 1 - \frac{v^-}{v^+}e^{\imath(2\gamma z)} \right) }
The fraction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{v^-}{v^+}} is called reflection coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{v^-}{v^+} = \Gamma e^{\imath \phi_z} = \frac{Z_L - Z_0}{Z_L + Z_0}}
which gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i(z,t) = = \frac{v^+}{Z_0} e^{\imath (\omega t - \gamma z)} \left( 1 - \Gamma e^{\imath(\phi_z +2\gamma z)} \right) }
The characteristic impedance is
Thus we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2 v}{dL^2} = \gamma^2 v } and similar for the current. The constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma^2 = (R+\imath \omega L)(G+\imath \omega C)} .
For lossless line Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R' = G' = 0} and for distortionless line Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R'/L' = G'/C'} . The voltage reflection coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = \frac{v^-}{v^+} = - \frac{i^-}{i^+} = \frac{Z_L - Z_0}{Z_L + Z_0} } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_0} is the characteristic impedance of transient line, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L} is the impedance of load (antenna). If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L= Z_0} , then the line is perfectly matched, and there is no mismatch loss and all power is transferred to the load (antenna).
- An open circuit: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L = \infty} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = +1} .
- A short circuit: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L = 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = -1} , and a phase reversal of the reflected voltage wave.
- A matched load: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_L = Z_0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma = 0} and no reflections.
The voltage standing wave ratio or VSWR
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{VSWR} = \frac{|V|_\text{max}}{||V|_\text{min}|} = \frac{1 + |\Gamma|}{1 - |\Gamma|} }
Siirtolinja (transmission line). Impedanssi. Koaksaalikaapelin impedanssi muodostuu sen kapasitiivisestä rakenteesta. Ei juuri resistiivistä häviötä (impedanssia) https://electronics.stackexchange.com/questions/543100/derivation-of-resistance-of-coaxial-cable. Koaksaalikaapelin εr
- 76.7 Ω
- 30 Ω
- The impedance of a centre-fed dipole antenna in free space is 73 Ω, so 75 Ω coax is commonly used for connecting shortwave antennas to receivers.
- Sometimes 300 Ω folded dipole antenna => 4:1 balun transformer is used.
twin-lead transmission lines: the characteristic impedance of is roughly 300 Ω.
Feeding length.
Some transmission lines are
- Coaxial cable
- Two-wire cable
- Microstrip line
- . . .
Skin Effect
The skin effect Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} . The higher the frequency, the more the currents are confined to the surface.
Balun
Velocity factor
| Velocity factor | Line type |
|---|---|
| 0.95 | Ladder line |
| 0.82 | Twin-lead |
| 0.79 | coaxial cable (foam dielectric) |
| 0.75 | RG-6 and RG-8 coaxial (thick) |
| 0.66 | RG-58 and RG-59 coaxial (thin) |