Brachistochrone

Introduction

To find the shape of the curve which the time is shortest possible. . .

We use WxMaxima to do the calculus part.

Theory

Variational Calculus and Euler--Lagrange Equation

The time from $P_{a}$ to $P_{b}$ is $t=\int _{P_{a}}^{P_{b}}{\frac {1}{v}}ds$ where $ds={\sqrt {1+y'{^{2}}}}dx$ is the Pythagorean distance measure and $v$ is determined from the the law of conservation of energy ${\frac {1}{2}}mv^{2}=mgy$. giving $v={\sqrt {2gy}}$. Plugging these in, we get $t=\int _{P_{a}}^{P_{b}}{\sqrt {\frac {1+y'^{2}}{2gy}}}dx=\int _{P_{a}}^{P_{b}}fdx$, where $f=f(y,y')$ is the function subject to variational consideration.

According to the Euler--Lagrange differential equation the stationary value is to be found, if E-L equation ${\frac {\partial f}{\partial y}}-{\frac {d}{dx}}{\frac {\partial f}{\partial y'}}=0$ is satisfied.

No Friction

Since $f$ does not depend on $x$, we may use the simplified E--L formula $f-y'{\frac {\partial f}{\partial y'}}=$ Constant. We get

${\frac {\partial f}{\partial y'}}={\frac {\partial }{\partial y'}}{\sqrt {\frac {1+y'^{2}}{2gy}}}={\frac {1}{\sqrt {2gy}}}{\frac {\partial }{\partial y'}}{\sqrt {1+y'^{2}}}={\frac {2y'}{\sqrt {2gy}}}{\frac {1}{2{\sqrt {1+y'^{2}}}}}$.

Thus, we have

$f-y'{\frac {\partial f}{\partial y'}}={\sqrt {\frac {1+y'{^{2}}}{2gy}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}=C$ So we have ${\frac {1+y'{^{2}}}{\sqrt {2gy(1+y'{^{2}})}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}={\frac {1}{\sqrt {2gy(1+y'{^{2}})}}}=C$ and multiplying this with the denominator and rearring, we have $y\left(1+y'^{2}\right)={\frac {1}{2gC^{2}}}=k^{2}$ by redefining the constant. The standard solution to this equation is given by

${\begin{aligned}x&={\frac {1}{2}}k^{2}(\theta -\sin \theta )\\y&={\frac {1}{2}}k^{2}(1-\cos \theta )\end{aligned}}$

and is the equation of a cycloid.

The same

energy : 1/2*m*v^2 = m*g*y;
v_sol : solve( energy, v);
v_sol : v_sol[2];
EL_f : rhs( sqrt(1+'diff(y,t)^2)/v_sol );
doof_dooyp : diff( EL_f, 'diff(y,t));
EL: EL_f - 'diff(y,t)*doof_dooyp = C;
radcan(%);
EL_dy : solve(EL, y);
ode2(EL_dy[1]^2,y,t);

but the ode2 solver cannot handle the nonlinear differential equation.

Rolling Ball: Angular momentum but no radius

The rotational energy is $E_{\text{rot}}={\frac {1}{2}}I\omega ^{2}$ and by applying non-slipping condition $v=\omega r$ we get $E_{\text{rot}}={\frac {v^{2}}{2r^{2}}}I$. Note that actually the ball is rolling on a curve, and thus the given slipping condition is only an approximation. The correct case is shown below in Chapter . ..

For the simplified case, the calculation is similar to the previous one, and using Maxima, we get

energy : 1/2*m*v^2 + 1/2*I*v^2/r^2= m*g*y;
. . .

gives

${\begin{aligned}{\frac {\sqrt {m\,{{r}^{2}}+I}}{{\sqrt {2gmy}}r\,{\sqrt {{{\left({\frac {d}{dt}}y\right)}^{2}}+1}}}}=C&&\Rightarrow &&y(1+y'{^{2}})={\frac {mr^{2}+I}{2gmr^{2}C^{2}}}=k_{1}^{2}\end{aligned}}$

and thus only the constant $k_{1}$ differs from the case with no angular momentum.

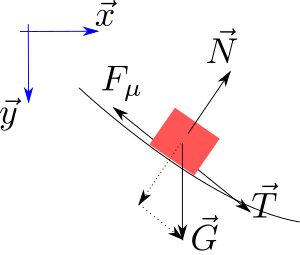
Friction

The forces on the path. Actually the sliding particle is infinitemal small.

The normal force follows the path, and thus is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec T = \frac{dx}{ds}\vec x + \frac{dy}{ds} \vec y } , but The friction depends on the normal force of the path. The normal force is perpendicular to the previous, thus we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec N = - \frac{dy}{ds}\vec x + \frac{dx}{ds} \vec y }

The conservation of energy does not apply here, but we have Newton's Second Law, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec F = m \frac{d \vec v}{dt}} . We need the components along the curve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} . Thus we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \vec F &= \vec G - \vec F_\mu \\ &= mg \frac{dy}{ds} - \mu mg \frac{dx}{ds} \end{align} }

Clearly, for the left hand side of NII we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\frac{dv}{dt} = m \frac{dv}{ds}\frac{ds}{dt} = m \frac{dv}{ds} v = mv \frac{dv}{ds} = m\frac12 \frac {d v^2}{ds} } , and by including the differential part only, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac12 v^2 &= g( y - \mu x ) \\ v&= \sqrt{2g(y-\mu x)} \end{align} }

and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} for the Euler--Lagrange equation is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \sqrt{ \frac{1+y'^{2}}{2g(y-\mu x)} } }

Euler--Lagrange

NII : 1/2*v^2 = g*(y(x)-mu*x);

v_sol : solve( NII, v);
v_sol : v_sol[2];

EL_f : rhs( sqrt(1+'diff(y(x),x)^2)/v_sol );
df_dy : diff(EL_f, y(x));
df_dyp : diff(EL_f, 'diff(y(x),x));
d_dx : diff( df_dyp, x);


EL : df_dy - d_dx = 0; 
Elrad : radcan( EL );

num( lhs(ELrad) )/sqrt(2)/sqrt(y(x)-mu*x)=0;
ratsimp(%);

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \left( 2 \mu x-2 \operatorname{y}(x)\right) \, \left( \frac{{{d}^{2}}}{d {{x}^{2}}} \operatorname{y}(x)\right) -\mu {{\left( \frac{d}{d x} \operatorname{y}(x)\right) }^{3}}-{{\left( \frac{d}{d x} \operatorname{y}(x)\right) }^{2}}-\mu \left( \frac{d}{d x} \operatorname{y}(x)\right) -1=0 \\ 2 \left( y - \mu x \right) y'' + \left( 1+ \left( y' \right)^2 \right) \left( 1 + \mu y' \right) =0 \end{align} }

Note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d }{dx}\left( y(x) - \mu x \right) } .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \frac{y'-\mu}{y-\mu x} = \frac{2(y'-\mu) y''}{(1+y'^{2})(1+\mu y')} }

The right hand side can be integrated:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \int \frac{y'-\mu}{y-\mu x} dx = -\ln |y - \mu x| + C_1 }

This can be reduced to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \operatorname{y}(x)-\mu x\right) \, \left( {{\left( \frac{d}{d x} \operatorname{y}(x)\right) }^{2}}+1\right) = C\, {{\left( \mu \left( \frac{d}{d x} \operatorname{y}(x)\right) +1\right) }^{2}} }

Rolling Ball with radius

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = \frac{r_\text{curve}+r}{r}\frac{d \alpha}{d t} - \frac{d\alpha}{dt} = \frac{\rho}{r} \frac{d\alpha}{dt} = \frac{v}{r} }

The conservation of energy:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle mgy = \frac12 mv^2 + \frac12 \frac25 m r^2 v^2/r^2 }

Beltrami Indentity

E-L states: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial L}{\partial y} = \frac{d}{dx}\frac{\partial L}{\partial y'}} , but Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dL}{dx} = y'\frac{\partial L}{\partial y} + y''\frac{\partial L}{\partial y'} + \frac{\partial L}{\partial x}} , and now Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial L/\partial x = 0} and by substituting the first result, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{d L}{d x} - ( y'\frac{d}{dx} \frac{\partial L}{\partial y'} + y''\frac{\partial L}{\partial y'} ) = 0 \\ \Leftrightarrow \\ \frac{dL}{dx} - \frac{d}{dx} \left( y' \frac{\partial L}{\partial y'} \right) = \frac{d}{dx}\left( L - y' \frac{\partial L}{\partial y'}\right) = 0 \end{align} }

and thus Beltrami follows.

References

https://mathworld.wolfram.com/BrachistochroneProblem.html

https://physicscourses.colorado.edu/phys3210/phys3210_sp20/lecture/lec04-lagrangian-mechanics/

http://hades.mech.northwestern.edu/images/e/e6/Legeza-MechofSolids2010.pdf

https://www.tau.ac.il/~flaxer/edu/course/computerappl/exercise/Brachistochrone%20Curve.pdf

https://mate.uprh.edu/~urmaa/reports/brach.pdf The Nonlinear Brachistochrone Problem with Friction Pablo V. Negr´on–Marrero∗ and B´arbara L. Santiago–Figueroa

https://medium.com/cantors-paradise/the-famous-problem-of-the-brachistochrone-8b955d24bdf7

https://wiki.math.ntnu.no/_media/tma4180/2015v/calcvar.pdf BASICS OF CALCULUS OF VARIATIONS MARKUS GRASMAIR

http://www.doiserbia.nb.rs/img/doi/0354-5180/2012/0354-51801204697M.pdf

http://info.ifpan.edu.pl/firststep/aw-works/fsV/parnovsky/parnovsky.pdf Some Generalisations of Brachistochrone Problem. A.S. Parnovsky

[https://arxiv.org/pdf/1604.03021.pdf Tautochrone and Brachistochrone Shape Solutions for Rocking Rigid Bodies. Patrick Glaschke April 12, 2016]

https://issuu.com/nameou/docs/math_seminar_paper A complete detailed solution to the brachistochrone problem. N. H. Nguyen.

https://arxiv.org/pdf/1908.02224.pdf Brachistochrone on a velodrome. GP Benham, C Cohen, E Brunet and C Clanet

https://arxiv.org/pdf/1712.04647.pdf On the brachistochrone of a fluid-filled cylinder. Srikanth Sarma Gurram, Sharan Raja, Pallab Sinha Mahapatra and Mahesh V. Panchagnula.

https://arxiv.org/pdf/1001.2181.pdf A Detailed Analysis of the Brachistochrone Problem R.Coleman

https://math.stackexchange.com/questions/3068293/euler-lagrange-equation-for-the-brachistochrone-problem-with-friction

https://math.stackexchange.com/questions/3685969/brachistochrone-problem-including-friction-reducing-a-differential-equation

https://www.jstor.org/stable/2974953?seq=1#metadata_info_tab_contents Exploring the Brachistochrone Problem. LaDawn Haws and Terry Kiser.