Brachistochrone

Introduction

To find the shape of the curve which the time is shortest possible. . .

Theory

Variational Calculus and Euler--Lagrange Equation

The time from $P_{a}$ to $P_{b}$ is $t=\int _{P_{a}}^{P_{b}}{\frac {1}{v}}ds$ where $ds={\sqrt {1+y'{^{2}}}}dx$ is the Pythagorean distance measure and $v$ is determined from the the law of conservation of energy ${\frac {1}{2}}mv^{2}=mgy$. giving $v={\sqrt {2gy}}$. Plugging these in, we get $t=\int _{P_{a}}^{P_{b}}{\sqrt {\frac {1+y'^{2}}{2gy}}}dx=\int _{P_{a}}^{P_{b}}fdx$, where $f=f(y,y')$ is the function subject to variational consideration.

According to the Euler--Lagrange differential equation the stationary value is to be found, if E-L equation ${\frac {\partial f}{\partial y}}-{\frac {d}{dx}}{\frac {\partial f}{\partial y'}}=0$ is satisfied.

No Friction

We get

${\frac {\partial f}{\partial y'}}={\frac {\partial }{\partial y'}}{\sqrt {\frac {1+y'^{2}}{2gy}}}={\frac {1}{\sqrt {2gy}}}{\frac {\partial }{\partial y'}}{\sqrt {1+y'^{2}}}={\frac {2y'}{\sqrt {2gy}}}{\frac {1}{2{\sqrt {1+y'^{2}}}}}$.

Since $f$ does not depend on $x$, we may use the simplified E--L formula $f-y'{\frac {\partial f}{\partial y'}}={\text{Constant}}$.

Thus, we have

$f-y'{\frac {\partial f}{\partial y'}}={\sqrt {\frac {1+y'{^{2}}}{2gy}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}=C$ So we have ${\frac {1+y'{^{2}}}{\sqrt {2gy(1+y'{^{2}})}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}={\frac {1}{\sqrt {2gy(1+y'{^{2}})}}}=C$ and multiplying this with the denominator and rearring, we have $y\left(1+y'^{2}\right)={\frac {1}{2gC^{2}}}=k^{2}$

by redefining the constant. The standard solution to this equation is given by

${\begin{aligned}x&={\frac {1}{2}}k^{2}(\theta -\sin \theta )\\y&={\frac {1}{2}}k^{2}(1-\cos \theta )\end{aligned}}$

and is the equation of a cycloid.

Rolling Ball: Angular momentum

The rotational energy is $E_{\text{rot}}={\frac {1}{2}}I\omega ^{2}$ and by applying non-slipping condition $v=\omega r$ we get $E_{\text{rot}}={\frac {v^{2}}{2r^{2}}}I$. The conservation energy states

${\begin{aligned}E_{\text{kin}}&=E_{\text{rot}}\\{\frac {1}{2}}mv^{2}+{\frac {v^{2}}{2r^{2}}}I&=mgy\\v^{2}&={\frac {mgy}{m+I/(2r^{2})}}\\&={\frac {2mgr^{2}}{2m+I}}\end{aligned}}$

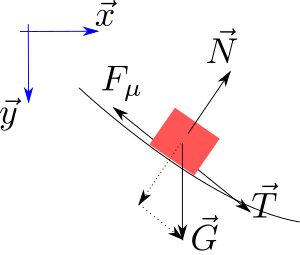
Friction

The forces on the path. Actually the sliding particle is infinitemal small.

The normal force follows the path, and thus is given by ${\vec {T}}={\frac {dx}{ds}}{\vec {x}}+{\frac {dy}{ds}}{\vec {y}}$, but The friction depends on the normal force of the path. The normal force is perpendicular to the previous, thus we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec N = - \frac{dy}{ds}\vec x + \frac{dx}{ds} \vec y }

The conservation of energy does not apply here, but we have Newton's Second Law, ${\vec {F}}=m{\frac {d{\vec {v}}}{dt}}$. We need the components along the curve $s$. Thus we have

${\begin{aligned}{\vec {F}}&={\vec {G}}-{\vec {F}}_{\mu }\\&=mg{\frac {dy}{ds}}-\mu mg{\frac {dx}{ds}}\end{aligned}}$

Clearly, for the left hand side of NII we have $m{\frac {dv}{dt}}=mv{\frac {dv}{ds}}=m{\frac {1}{2}}{\frac {dv^{2}}{ds}}$, and by including the differential part only, we have

${\begin{aligned}{\frac {1}{2}}v^{2}&=g(y-\mu x)\\v&={\sqrt {2g(y-\mu x)}}\end{aligned}}$

and $f$ for the Euler--Lagrange equation is $f={\sqrt {\frac {1+y'^{2}}{2g(y-\mu x)}}}$

Euler--Lagrange

${\frac {\partial f}{\partial y}}-{\frac {d}{dt}}{\frac {\partial f}{\partial y'}}=0$

${\begin{aligned}{\frac {\partial f}{\partial y}}&={\sqrt {\frac {1+y'^{2}}{2g}}}{\frac {\partial }{\partial y}}(y-\mu x)^{-1/2}\\&={\sqrt {\frac {1+y'^{2}}{2g}}}{\frac {-1}{2(y-\mu x)^{3/2}}}\\&=-{\frac {1}{2(y-\mu x)}}{\sqrt {\frac {1+y'^{2}}{2g(y-\mu x)}}}\\\end{aligned}}$

${\begin{aligned}{\frac {\partial f}{\partial y'}}&={\frac {1}{\sqrt {2g(y-\mu x)}}}{\frac {\partial }{\partial y}}{\sqrt {1+y'^{2}}}\\&={\frac {y'}{2{\sqrt {2g(y-\mu x)}}{\sqrt {1+y'^{2}}}}}\\\end{aligned}}$

${\begin{aligned}{\frac {d}{dt}}{\frac {\partial f}{\partial y'}}&={\frac {-\left(2y''{\sqrt {2g(y-\mu x)}}{\frac {y'}{\sqrt {1+y'^{2}}}}+{\sqrt {2}}g(y'-\mu x'){\frac {\sqrt {1+y'^{2}}}{\sqrt {g(y-\mu x)}}}\right)y'+2{\sqrt {2}}y''{\sqrt {y-\mu x}}{\sqrt {1+y'^{2}}}}{\left(2{\sqrt {2g(y-\mu x)}}{\sqrt {1+y'^{2}}}\right)^{2}}}\end{aligned}}$

Plugging these into EL we have

${\begin{aligned}-{\frac {1}{2(y-\mu x)}}{\sqrt {\frac {1+y'^{2}}{2g(y-\mu x)}}}&={\frac {-\left(2y''{\sqrt {2g(y-\mu x)}}{\frac {y'}{\sqrt {1+y'^{2}}}}+{\sqrt {2}}g(y'-\mu x'){\frac {\sqrt {1+y'^{2}}}{\sqrt {g(y-\mu x)}}}\right)y'+2{\sqrt {2}}y''{\sqrt {y-\mu x}}{\sqrt {1+y'^{2}}}}{\left(2{\sqrt {2g(y-\mu x)}}{\sqrt {1+y'^{2}}}\right)^{2}}}\\\\-4g({\frac {(1+y'^{2})^{3/2}}{\sqrt {2g(y-\mu x)}}}&=-\left(2y''{\sqrt {2g(y-\mu x)}}{\frac {y'}{\sqrt {1+y'^{2}}}}+{\sqrt {2}}g(y'-\mu x'){\frac {\sqrt {1+y'^{2}}}{\sqrt {g(y-\mu x)}}}\right)y'+2{\sqrt {2}}y''{\sqrt {y-\mu x}}{\sqrt {1+y'^{2}}}\\\end{aligned}}$

References

https://mathworld.wolfram.com/BrachistochroneProblem.html

https://physicscourses.colorado.edu/phys3210/phys3210_sp20/lecture/lec04-lagrangian-mechanics/

http://hades.mech.northwestern.edu/images/e/e6/Legeza-MechofSolids2010.pdf

https://www.tau.ac.il/~flaxer/edu/course/computerappl/exercise/Brachistochrone%20Curve.pdf