Draw a parabola using a pen attached to a robot

Introduction

How to use robot to draw mathematical shapes? We start by doing a parabola.

Aim

Triangles, trigonometric functions, Pythagorean theorem, series, limit, differential.

Center of gravity

Robot

Almost any robot will do, but this example is done using Asimov 2/ Verne. Note that some exercises requires a different robot.

Sensors

A gyroscope sensor is used in addition to servo motors.

Theory

The robot follows the blue line.

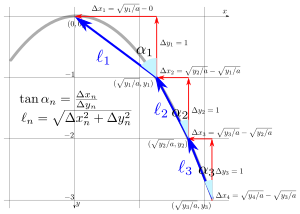
A parabola is a function (or mapping) $y=ax^{2}$ (without the constant). The inverse function of the positive root is $x={\sqrt {y/a}}$. We drive the robot in $N$ steps to the vertex, see the image.

The angle $\alpha _{n}$ of $n$th slope with respect to the resetting can calculated using $tan$ function. The distance travelled by the robot can be obtained using trigonometric functions or Pythagorean theorem.

Note that all parabolas are similar, see is only One True Parabola by Matt Parker

Python

The code should be tested on a computer first. The for plotting the linegraph of the parabola is given at Draw a parabola (python).

Example Code

The script can be run by pressing F5 as is shown on the page Install ev3dev.

#!/usr/bin/env python3
# https://sites.google.com/site/ev3devpython/

from ev3dev2.sensor.lego import GyroSensor
from ev3dev2.motor import MoveSteering, OUTPUT_B, OUTPUT_C
import math

import os
os.system('setfont Lat15-TerminusBold32x16') 

steer = MoveSteering(OUTPUT_B, OUTPUT_C)
gy = GyroSensor() 
gy.reset()

a = -.1
for i in range(-5,1):
    y1 = i
    y0 = i-1
    Dy = y1-y0
    Dx = math.sqrt(y1/a) - math.sqrt(y0/a)
    alpha = math.atan(Dx/Dy)/3.14159*180    #In degrees
    l = math.sqrt(Dy**2 + Dx**2)
    print( gy.angle, alpha )

    #Steer to the angle:
    while gy.angle > alpha:
        print( gy.angle, alpha )
        steer.on(steering=-100, speed=10)

    steer.on_for_rotations(steering=0, speed=-10, rotations=l, block=True)

Exercises

• Use more points than those provided here.
• Implement proportional gyroscope follower so that the robot follows the correct angle even if the robot is disturbed.
• Apply trigonometric functions to calculate $\ell _{n}$.
• Notice that the position of pen is not optimal. Where should the pen be located? Modify the robot such that you can put the pen into an optimal position.
• Make the parabola symmetric, thus make the robot turn more.
• Instead of using triangles, try making a limit and using the differential of the curve.
• Apply the method to draw 3th and 4th order polynomials, too.

Back to Mahtavaa Matematiikkaa 2020