Qiskit

Introduction

https://quantum-computing.ibm.com/

https://quantum-computing.ibm.com/challenges/fall-2020

https://quantum-computing.ibm.com/jupyter/user/IBMQuantumChallenge2020/week-1/ex_1a_en.ipynb

Installation

Installation https://qiskit.org/documentation/install.html

conda create -n qiskit python=3
conda activate qiskit
pip install qiskit /////_OR_////// pip install qiskit[visualization]

Did not work using Python 3.9. Instead, downgrade to Python 3.8.3 in your virtual environment.

conda create -n qiskit python=3
conda activate qiskit
conda install python=3.8.3
pip install qiskit ///////_OR_////// pip install qiskit[visualization]

Set up the Spyder IDE https://stackoverflow.com/questions/30170468/how-to-run-spyder-in-virtual-environment#47615445

Setting Up Qiskit

https://qiskit.org/textbook/ch-states/representing-qubit-states.html

from qiskit import QuantumCircuit, execute, Aer

qc = QuantumCircuit(1)  # Create a quantum circuit with one qubit
initial_state = [0,1]   # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
qc.draw('text')  # Let's view our circuit (text drawing is required for the 'Initialize' gate due to a known bug in qiskit)

backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
result = execute(qc,backend).result() # Do the simulation, returning the result
out_state = result.get_statevector()
print(out_state) # Display the output state vector

from qiskit.visualization import plot_histogram, plot_bloch_vector

qc.measure_all()
qc.draw()
result = execute(qc,backend).result()
counts = result.get_counts()
plot_histogram(counts)

Take superposition as initial state

initial_state = [1/sqrt(2), 1j/sqrt(2)]  # Define state |q>

The Bloch Sphere

from qiskit_textbook.widgets import plot_bloch_vector_spherical
coords = [pi/2,0,1] # [Theta, Phi, Radius]
plot_bloch_vector_spherical(coords) # Bloch Vector with spherical coordinates

Qiskit allows measuring in the Z-basis, only.

Theory

Quantum operations are reversible, thus the reversible computing. That makes some complications to the gate design.

Three Qubits

Toffoli gate made using CNOTs.

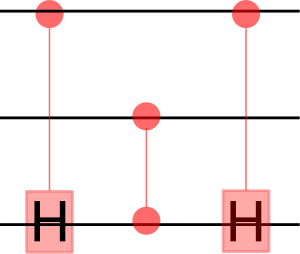
For universal computations we need more qubits. Eg. the AND gate is not reversible, and thus we need eg. Toffoli (CCNOT) gate.

Toffoli gate performs $X$ on target qubit if both control cubits are set to state $|1\rangle$.

qc = QuantumCircuit(3)
a = 0
b = 1
t = 2
# Toffoli with control qubits a and b and target t
qc.ccx(a,b,t)
qc.draw()

Toffoli using CNOTs uses fewer gates.

qc = QuantumCircuit(3)
qc.ch(a,t)
qc.cz(b,t)
qc.ch(a,t)
qc.draw()

AND gate is Toffoli gate with . . .

The nand gate

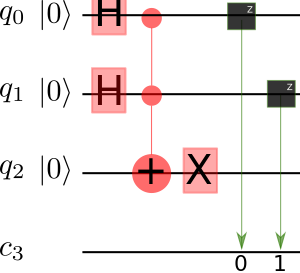
${\text{CCNOT}}(x,y,z)=(x,y,(x\land y)\otimes z)$ gives the reversible NAND ${\text{NAND}}(x,y)={\text{CCNOT}}(x,y,1)=(x,y,(x\land y)\otimes 1)$

NAND gate is

Exercises

Week 1

Week 2

Week 3