Line 162:
Line 162: {\left( 2 \sqrt{ 2g(y- \mu x) }\sqrt{1+y'^{2}} \right)^2 } \\
{\left( 2 \sqrt{ 2g(y- \mu x) }\sqrt{1+y'^{2}} \right)^2 } \\
\\
\\
- 4g ( \frac{ ( 1+y'^{2})^{3/2}}{ \sqrt{2g(y-\mu x)} }
- 4g \frac{ ( 1+y'^{2})^{3/2}}{ \sqrt{2g(y-\mu x)} }
&=
&=
-\left( 2 y''\sqrt{2g(y-\mu x)} \frac{y'}{\sqrt{1+y'^{2}}} + \sqrt2 g ( y' - \mu x' )\frac{\sqrt{1+y'^{2}}}{\sqrt{g(y-\mu x)}} \right)y'
-\left( 2 y''\sqrt{2g(y-\mu x)} \frac{y'}{\sqrt{1+y'^{2}}} + \sqrt2 g ( y' - \mu x' )\frac{\sqrt{1+y'^{2}}}{\sqrt{g(y-\mu x)}} \right)y'
Introduction To find the shape of the curve which the time is shortest possible. . .
Theory Variational Calculus and Euler--Lagrange Equation The time from
P
a
{\displaystyle P_{a}}
P
b
{\displaystyle P_{b}}
t
=
∫
P
a
P
b
1
v
d
s
{\displaystyle t=\int _{P_{a}}^{P_{b}}{\frac {1}{v}}ds}
d
s
=
1
+
y
′
2
d
x
{\displaystyle ds={\sqrt {1+y'{^{2}}}}dx}
v
{\displaystyle v}
1
2
m
v
2
=
m
g
y
{\displaystyle {\frac {1}{2}}mv^{2}=mgy}
v
=
2
g
y
{\displaystyle v={\sqrt {2gy}}}
t
=
∫
P
a
P
b
1
+
y
′
2
2
g
y
d
x
=
∫
P
a
P
b
f
d
x
{\displaystyle t=\int _{P_{a}}^{P_{b}}{\sqrt {\frac {1+y'^{2}}{2gy}}}dx=\int _{P_{a}}^{P_{b}}fdx}
f
=
f
(
y
,
y
′
)
{\displaystyle f=f(y,y')}
According to the Euler--Lagrange differential equation the stationary value is to be found, if E-L equation
∂
f
∂
y
−
d
d
x
∂
f
∂
y
′
=
0
{\displaystyle {\frac {\partial f}{\partial y}}-{\frac {d}{dx}}{\frac {\partial f}{\partial y'}}=0}
No Friction We get
∂
f
∂
y
′
=
∂
∂
y
′
1
+
y
′
2
2
g
y
=
1
2
g
y
∂
∂
y
′
1
+
y
′
2
=
2
y
′
2
g
y
1
2
1
+
y
′
2
{\displaystyle {\frac {\partial f}{\partial y'}}={\frac {\partial }{\partial y'}}{\sqrt {\frac {1+y'^{2}}{2gy}}}={\frac {1}{\sqrt {2gy}}}{\frac {\partial }{\partial y'}}{\sqrt {1+y'^{2}}}={\frac {2y'}{\sqrt {2gy}}}{\frac {1}{2{\sqrt {1+y'^{2}}}}}}
Since
f
{\displaystyle f}
x
{\displaystyle x}
f
−
y
′
∂
f
∂
y
′
=
Constant
{\displaystyle f-y'{\frac {\partial f}{\partial y'}}={\text{Constant}}}
Thus, we have
f
−
y
′
∂
f
∂
y
′
=
1
+
y
′
2
2
g
y
−
y
′
2
2
g
y
1
+
y
′
2
=
C
{\displaystyle f-y'{\frac {\partial f}{\partial y'}}={\sqrt {\frac {1+y'{^{2}}}{2gy}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}=C}
1
+
y
′
2
2
g
y
(
1
+
y
′
2
)
−
y
′
2
2
g
y
1
+
y
′
2
=
1
2
g
y
(
1
+
y
′
2
)
=
C
{\displaystyle {\frac {1+y'{^{2}}}{\sqrt {2gy(1+y'{^{2}})}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}={\frac {1}{\sqrt {2gy(1+y'{^{2}})}}}=C}
y
(
1
+
y
′
2
)
=
1
2
g
C
2
=
k
2
{\displaystyle y\left(1+y'^{2}\right)={\frac {1}{2gC^{2}}}=k^{2}}
by redefining the constant. The standard solution to this equation is given by
x
=
1
2
k
2
(
θ
−
sin
θ
)
y
=
1
2
k
2
(
1
−
cos
θ
)
{\displaystyle {\begin{aligned}x&={\frac {1}{2}}k^{2}(\theta -\sin \theta )\\y&={\frac {1}{2}}k^{2}(1-\cos \theta )\end{aligned}}}
and is the equation of a cycloid.
Rolling Ball: Angular momentum The rotational energy is
E
rot
=
1
2
I
ω
2
{\displaystyle E_{\text{rot}}={\frac {1}{2}}I\omega ^{2}}
v
=
ω
r
{\displaystyle v=\omega r}
E
rot
=
v
2
2
r
2
I
{\displaystyle E_{\text{rot}}={\frac {v^{2}}{2r^{2}}}I}
E
kin
=
E
rot
1
2
m
v
2
+
v
2
2
r
2
I
=
m
g
y
v
2
=
m
g
y
m
+
I
/
(
2
r
2
)
=
2
m
g
r
2
2
m
+
I
{\displaystyle {\begin{aligned}E_{\text{kin}}&=E_{\text{rot}}\\{\frac {1}{2}}mv^{2}+{\frac {v^{2}}{2r^{2}}}I&=mgy\\v^{2}&={\frac {mgy}{m+I/(2r^{2})}}\\&={\frac {2mgr^{2}}{2m+I}}\end{aligned}}}
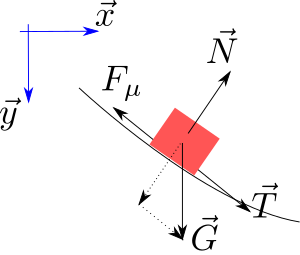
Friction The forces on the path. Actually the sliding particle is infinitemal small. The normal force follows the path, and thus is given by
T
→
=
d
x
d
s
x
→
+
d
y
d
s
y
→
{\displaystyle {\vec {T}}={\frac {dx}{ds}}{\vec {x}}+{\frac {dy}{ds}}{\vec {y}}}
N
→
=
−
d
y
d
s
x
→
+
d
x
d
s
y
→
{\displaystyle {\vec {N}}=-{\frac {dy}{ds}}{\vec {x}}+{\frac {dx}{ds}}{\vec {y}}}
The conservation of energy does not apply here, but we have Newton's Second Law,
F
→
=
m
d
v
→
d
t
{\displaystyle {\vec {F}}=m{\frac {d{\vec {v}}}{dt}}}
s
{\displaystyle s}
F
→
=
G
→
−
F
→
μ
=
m
g
d
y
d
s
−
μ
m
g
d
x
d
s
{\displaystyle {\begin{aligned}{\vec {F}}&={\vec {G}}-{\vec {F}}_{\mu }\\&=mg{\frac {dy}{ds}}-\mu mg{\frac {dx}{ds}}\end{aligned}}}
Clearly, for the left hand side of NII we have
m
d
v
d
t
=
m
v
d
v
d
s
=
m
1
2
d
v
2
d
s
{\displaystyle m{\frac {dv}{dt}}=mv{\frac {dv}{ds}}=m{\frac {1}{2}}{\frac {dv^{2}}{ds}}}
1
2
v
2
=
g
(
y
−
μ
x
)
v
=
2
g
(
y
−
μ
x
)
{\displaystyle {\begin{aligned}{\frac {1}{2}}v^{2}&=g(y-\mu x)\\v&={\sqrt {2g(y-\mu x)}}\end{aligned}}}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f}
for the Euler--Lagrange equation is
f
=
1
+
y
′
2
2
g
(
y
−
μ
x
)
{\displaystyle f={\sqrt {\frac {1+y'^{2}}{2g(y-\mu x)}}}}
Euler--Lagrange
∂
f
∂
y
−
d
d
t
∂
f
∂
y
′
=
0
{\displaystyle {\frac {\partial f}{\partial y}}-{\frac {d}{dt}}{\frac {\partial f}{\partial y'}}=0}
∂
f
∂
y
=
1
+
y
′
2
2
g
∂
∂
y
(
y
−
μ
x
)
−
1
/
2
=
1
+
y
′
2
2
g
−
1
2
(
y
−
μ
x
)
3
/
2
=
−
1
2
(
y
−
μ
x
)
1
+
y
′
2
2
g
(
y
−
μ
x
)
{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial y}}&={\sqrt {\frac {1+y'^{2}}{2g}}}{\frac {\partial }{\partial y}}(y-\mu x)^{-1/2}\\&={\sqrt {\frac {1+y'^{2}}{2g}}}{\frac {-1}{2(y-\mu x)^{3/2}}}\\&=-{\frac {1}{2(y-\mu x)}}{\sqrt {\frac {1+y'^{2}}{2g(y-\mu x)}}}\\\end{aligned}}}
∂
f
∂
y
′
=
1
2
g
(
y
−
μ
x
)
∂
∂
y
1
+
y
′
2
=
y
′
2
2
g
(
y
−
μ
x
)
1
+
y
′
2
{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial y'}}&={\frac {1}{\sqrt {2g(y-\mu x)}}}{\frac {\partial }{\partial y}}{\sqrt {1+y'^{2}}}\\&={\frac {y'}{2{\sqrt {2g(y-\mu x)}}{\sqrt {1+y'^{2}}}}}\\\end{aligned}}}
d
d
t
∂
f
∂
y
′
=
−
(
2
y
″
2
g
(
y
−
μ
x
)
y
′
1
+
y
′
2
+
2
g
(
y
′
−
μ
x
′
)
1
+
y
′
2
g
(
y
−
μ
x
)
)
y
′
+
2
2
y
″
y
−
μ
x
1
+
y
′
2
(
2
2
g
(
y
−
μ
x
)
1
+
y
′
2
)
2
{\displaystyle {\begin{aligned}{\frac {d}{dt}}{\frac {\partial f}{\partial y'}}&={\frac {-\left(2y''{\sqrt {2g(y-\mu x)}}{\frac {y'}{\sqrt {1+y'^{2}}}}+{\sqrt {2}}g(y'-\mu x'){\frac {\sqrt {1+y'^{2}}}{\sqrt {g(y-\mu x)}}}\right)y'+2{\sqrt {2}}y''{\sqrt {y-\mu x}}{\sqrt {1+y'^{2}}}}{\left(2{\sqrt {2g(y-\mu x)}}{\sqrt {1+y'^{2}}}\right)^{2}}}\end{aligned}}}
Plugging these into EL we have
−
1
2
(
y
−
μ
x
)
1
+
y
′
2
2
g
(
y
−
μ
x
)
=
−
(
2
y
″
2
g
(
y
−
μ
x
)
y
′
1
+
y
′
2
+
2
g
(
y
′
−
μ
x
′
)
1
+
y
′
2
g
(
y
−
μ
x
)
)
y
′
+
2
2
y
″
y
−
μ
x
1
+
y
′
2
(
2
2
g
(
y
−
μ
x
)
1
+
y
′
2
)
2
−
4
g
(
1
+
y
′
2
)
3
/
2
2
g
(
y
−
μ
x
)
=
−
(
2
y
″
2
g
(
y
−
μ
x
)
y
′
1
+
y
′
2
+
2
g
(
y
′
−
μ
x
′
)
1
+
y
′
2
g
(
y
−
μ
x
)
)
y
′
+
2
2
y
″
y
−
μ
x
1
+
y
′
2
{\displaystyle {\begin{aligned}-{\frac {1}{2(y-\mu x)}}{\sqrt {\frac {1+y'^{2}}{2g(y-\mu x)}}}&={\frac {-\left(2y''{\sqrt {2g(y-\mu x)}}{\frac {y'}{\sqrt {1+y'^{2}}}}+{\sqrt {2}}g(y'-\mu x'){\frac {\sqrt {1+y'^{2}}}{\sqrt {g(y-\mu x)}}}\right)y'+2{\sqrt {2}}y''{\sqrt {y-\mu x}}{\sqrt {1+y'^{2}}}}{\left(2{\sqrt {2g(y-\mu x)}}{\sqrt {1+y'^{2}}}\right)^{2}}}\\\\-4g{\frac {(1+y'^{2})^{3/2}}{\sqrt {2g(y-\mu x)}}}&=-\left(2y''{\sqrt {2g(y-\mu x)}}{\frac {y'}{\sqrt {1+y'^{2}}}}+{\sqrt {2}}g(y'-\mu x'){\frac {\sqrt {1+y'^{2}}}{\sqrt {g(y-\mu x)}}}\right)y'+2{\sqrt {2}}y''{\sqrt {y-\mu x}}{\sqrt {1+y'^{2}}}\\\end{aligned}}}
Rolling Ball with radius References https://mathworld.wolfram.com/BrachistochroneProblem.html
https://physicscourses.colorado.edu/phys3210/phys3210_sp20/lecture/lec04-lagrangian-mechanics/
http://hades.mech.northwestern.edu/images/e/e6/Legeza-MechofSolids2010.pdf
https://www.tau.ac.il/~flaxer/edu/course/computerappl/exercise/Brachistochrone%20Curve.pdf
