Line 88:
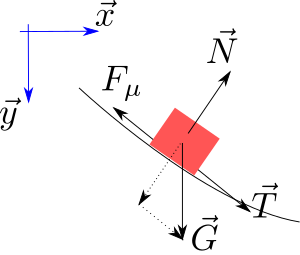
Line 88: [[File:Brac normalforce.svg|thumb|The Forces on the path. Actually the sliding particle is infinitemal small. ]]
[[File:Brac normalforce.svg|thumb|The Forces on the path. Actually the sliding particle is infinitemal small. ]]
The friction depends on the normal force of the path. The normal force is
The normal force follows the path, and thus is given by
<math>
\vec T = \frac{dx}{ds}\vec x + \frac{dy}{ds} \vec y
</math>, but The friction depends on the normal force of the path. The normal force is perpendicular to the previous, thus we have
<math>
<math>
\vec N = - \frac{dy}{ds}\vec x + \frac{dx}{ds} \vec y
\vec N = - \frac{dy}{ds}\vec x + \frac{dx}{ds} \vec y
</math>
The cross product of of normal force and tangential force is zero, giving e.g.
<math>
\vec T = \frac{dx}{ds}\vec x + \frac{dy}{ds} \vec y
</math>
</math>
Revision as of 10:37, 20 February 2021
Introduction To find the shape of the curve which the time is shortest possible. . .
Theory Variational Calculus and Euler--Lagrange Equation The time from
P
a
{\displaystyle P_{a}}
P
b
{\displaystyle P_{b}}
t
=
∫
P
a
P
b
1
v
d
s
{\displaystyle t=\int _{P_{a}}^{P_{b}}{\frac {1}{v}}ds}
d
s
=
1
+
y
′
2
d
x
{\displaystyle ds={\sqrt {1+y'{^{2}}}}dx}
v
{\displaystyle v}
1
2
m
v
2
=
m
g
y
{\displaystyle {\frac {1}{2}}mv^{2}=mgy}
v
=
2
g
y
{\displaystyle v={\sqrt {2gy}}}
t
=
∫
P
a
P
b
1
+
y
′
2
2
g
y
d
x
=
∫
P
a
P
b
f
d
x
{\displaystyle t=\int _{P_{a}}^{P_{b}}{\sqrt {\frac {1+y'^{2}}{2gy}}}dx=\int _{P_{a}}^{P_{b}}fdx}
f
=
f
(
y
,
y
′
)
{\displaystyle f=f(y,y')}
According to the Euler--Lagrange differential equation the stationary value is to be found, if E-L equation
∂
f
∂
y
−
d
d
x
∂
f
∂
y
′
=
0
{\displaystyle {\frac {\partial f}{\partial y}}-{\frac {d}{dx}}{\frac {\partial f}{\partial y'}}=0}
No Friction We get
∂
f
∂
y
′
=
∂
∂
y
′
1
+
y
′
2
2
g
y
=
1
2
g
y
∂
∂
y
′
1
+
y
′
2
=
2
y
′
2
g
y
1
2
1
+
y
′
2
{\displaystyle {\frac {\partial f}{\partial y'}}={\frac {\partial }{\partial y'}}{\sqrt {\frac {1+y'^{2}}{2gy}}}={\frac {1}{\sqrt {2gy}}}{\frac {\partial }{\partial y'}}{\sqrt {1+y'^{2}}}={\frac {2y'}{\sqrt {2gy}}}{\frac {1}{2{\sqrt {1+y'^{2}}}}}}
Since
f
{\displaystyle f}
x
{\displaystyle x}
f
−
y
′
∂
f
∂
y
′
=
Constant
{\displaystyle f-y'{\frac {\partial f}{\partial y'}}={\text{Constant}}}
Thus, we have
f
−
y
′
∂
f
∂
y
′
=
1
+
y
′
2
2
g
y
−
y
′
2
2
g
y
1
+
y
′
2
=
C
{\displaystyle f-y'{\frac {\partial f}{\partial y'}}={\sqrt {\frac {1+y'{^{2}}}{2gy}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}=C}
1
+
y
′
2
2
g
y
(
1
+
y
′
2
)
−
y
′
2
2
g
y
1
+
y
′
2
=
1
2
g
y
(
1
+
y
′
2
)
=
C
{\displaystyle {\frac {1+y'{^{2}}}{\sqrt {2gy(1+y'{^{2}})}}}-{\frac {y'{^{2}}}{{\sqrt {2gy}}{\sqrt {1+y'^{2}}}}}={\frac {1}{\sqrt {2gy(1+y'{^{2}})}}}=C}
y
(
1
+
y
′
2
)
=
1
2
g
C
2
=
k
2
{\displaystyle y\left(1+y'^{2}\right)={\frac {1}{2gC^{2}}}=k^{2}}
by redefining the constant. The standard solution to this equation is given by
x
=
1
2
k
2
(
θ
−
sin
θ
)
y
=
1
2
k
2
(
1
−
cos
θ
)
{\displaystyle {\begin{aligned}x&={\frac {1}{2}}k^{2}(\theta -\sin \theta )\\y&={\frac {1}{2}}k^{2}(1-\cos \theta )\end{aligned}}}
and is the equation of a cycloid.
Rolling Ball: Angular momentum The rotational energy is
E
rot
=
1
2
I
ω
2
{\displaystyle E_{\text{rot}}={\frac {1}{2}}I\omega ^{2}}
v
=
ω
r
{\displaystyle v=\omega r}
E
rot
=
v
2
2
r
2
I
{\displaystyle E_{\text{rot}}={\frac {v^{2}}{2r^{2}}}I}
E
kin
=
E
rot
1
2
m
v
2
+
v
2
2
r
2
I
=
m
g
y
v
2
=
m
g
y
m
+
I
/
(
2
r
2
)
=
2
m
g
r
2
2
m
+
I
{\displaystyle {\begin{aligned}E_{\text{kin}}&=E_{\text{rot}}\\{\frac {1}{2}}mv^{2}+{\frac {v^{2}}{2r^{2}}}I&=mgy\\v^{2}&={\frac {mgy}{m+I/(2r^{2})}}\\&={\frac {2mgr^{2}}{2m+I}}\end{aligned}}}
Thus, the path shape is same, than previous.
Friction The Forces on the path. Actually the sliding particle is infinitemal small. The normal force follows the path, and thus is given by
T
→
=
d
x
d
s
x
→
+
d
y
d
s
y
→
{\displaystyle {\vec {T}}={\frac {dx}{ds}}{\vec {x}}+{\frac {dy}{ds}}{\vec {y}}}
N
→
=
−
d
y
d
s
x
→
+
d
x
d
s
y
→
{\displaystyle {\vec {N}}=-{\frac {dy}{ds}}{\vec {x}}+{\frac {dx}{ds}}{\vec {y}}}
Rolling Ball with radius References https://mathworld.wolfram.com/BrachistochroneProblem.html
https://physicscourses.colorado.edu/phys3210/phys3210_sp20/lecture/lec04-lagrangian-mechanics/
http://hades.mech.northwestern.edu/images/e/e6/Legeza-MechofSolids2010.pdf
https://www.tau.ac.il/~flaxer/edu/course/computerappl/exercise/Brachistochrone%20Curve.pdf