Logo or turtle drawing: Difference between revisions
No edit summary |
No edit summary |
||
| Line 21: | Line 21: | ||
== Theory == | == Theory == | ||
[[File: | [[File:RotatingWheel2.svg|thumb|The distance travelled by a rotating wheel is <math>2\pi r</math>.]] | ||
The Asimov 2/ Verne robot travels <math>2\pi 57</math> mm <math>358</math> mm on one full turn, as the diameter of the wheel is <math>57</math> mm. First design the plotting on a paper (or using computer, eg. [http://www.inkscape.org Inkscape] is a good program) and then convert the distances to rotations. | |||
Usually it is easier to code if the speed is lower. Use only speed 10 or 15. The Asimov/ Verne 2 robot turns exactly (about) 90 degrees when XXXXX | Usually it is easier to code if the speed is lower. Use only speed 10 or 15. The Asimov/ Verne 2 robot turns exactly (about) 90 degrees when XXXXX | ||
Revision as of 10:33, 17 October 2020
Introduction
Drawing on a large paper using a robot is funny and involving. Use a large paper and try to stay on the paper. Logo programming is oldie but goodie.
Aim
Geometrical shapes, diameter of the circle, basic programming.
Center of gravity, steering.
Robot
Almost any robot will do. We use Asimov 2/ Verne robot with a pen attached to the front part of the robot.
Sensors
No sensors is used, except the servo motor.
Example Video
Theory
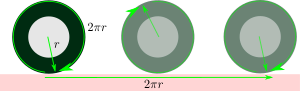
The Asimov 2/ Verne robot travels mm mm on one full turn, as the diameter of the wheel is mm. First design the plotting on a paper (or using computer, eg. Inkscape is a good program) and then convert the distances to rotations.
Usually it is easier to code if the speed is lower. Use only speed 10 or 15. The Asimov/ Verne 2 robot turns exactly (about) 90 degrees when XXXXX
Example Code
Exercises
- Draw a square.
- Draw a house.
- Draw a giraffe.
- Note that the pen draws a wrong line when the robot rotates. How fix to that?
- Try to implement gyroscope to better stay in the given direction.
Back to Mahtavaa Matematiikkaa 2020




