Velocity, acceleration and jerk

Introduction

The Newton Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=ma} force rule states that force and acceleration are proportionally related. Is it possible to accelerate without noticing the jerk? The method is used in elevators, for example, and hopefully in modern (electric) cars.

We consider the acceleration the robot is subjected to while accelerating it using different acceleration functions.

Robot

Almost any robot will be ok, we use Asimov 2/ Verne.

Sensor

The Vernier acceleration sensor with the NXT Adapter is used. The sensor is attached to port number 4.

Very simple test program to see what are the measured values is shown below. The values are in arbitrary scale, and need to be normalized. We found, that the

#!/usr/bin/env python3
# https://sites.google.com/site/ev3devpython/

from ev3dev2.sensor import *
from ev3dev2.sensor import INPUT_4

import time
import os
import csv 

os.system('setfont Lat15-TerminusBold32x16')  # Try this larger font

p = Sensor( INPUT_4 )
p.mode="ANALOG-1"

def measureAcc(p):
    acc = p.value(0)
    return acc

f = open('acc.csv',"w")
writer = csv.writer(f) 
tstep = 0.001

while True:
    acc = measureAcc(p)
    print( acc )
    writer.writerow((time.time(), acc ))
    time.sleep( tstep )

The resulted file acc.csv is then manually downloaded into a computer, and plotted using Python Pandas:

import pandas as pd
import matplotlib.pyplot as plt

# Read CSV file into DataFrame df
df = pd.read_csv('acc.csv', index_col=0)

# Show thedataframe
print(df)
plt.plot(df)

Theory

The time derivative of position is velocity, then we have acceleration, and the derivative of acceleration is called jerk, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d a}{dt} = j } Then we have snap, crackle and pop.

See the Wikipedia page on the physiological_effects of jerk. Anyway, there might be jerky rides.

We measure the acceleration of robot, and use a numerical differential method to estimate the jerk. We use the symmetric differential;

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j(t) = \frac{d a}{dt} = \frac{f(t-h) + f(t+h)}{2h} } in which the first-order error cancels, and the error is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac16 f^{(3)}(x) h^2} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t-h < x < t+h} .

We will start from zero to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0 = 5000} ms where the speed should be at maximum value, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=100} .

Standard Scheme

The ev3dev Python standard scheme is . . .

Linear acceleration

The Linear Acceleration

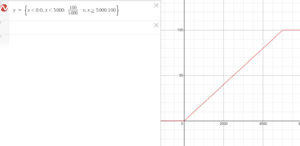
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(t) = \begin{cases} \frac L{t_0} t && \text{if } t< t_0 \\ L && \text{if } t\geq t_0 \end{cases} }

because the continuity constraint Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle at_0 = L} gives that $a=L/t_{0}$. The graph is shown on Desmos .

Sinusoidal acceleration

Sine acceleration

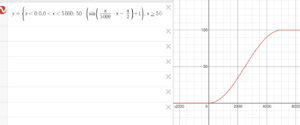
The sine curve is a harmonic motion between -1 and 1 with period $2\pi$. We use only one period, and scale that to correct acceleration function. The sine accelerates rather smoothly.

$v(t)={\begin{cases}{\frac {L}{2}}(\sin({\frac {\pi }{t_{0}}}t-{\frac {\pi }{2}})+1)&&{\text{if }}t<t_{0}\\L&&{\text{if }}t\geq t_{0}\end{cases}}$

See the interactive Desmos graph.

Logistic Curve

The logistic Curve with parameters.

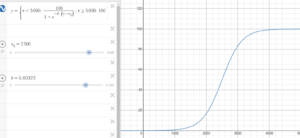
A logistic function is S-shaped curve (or sigmoid curve) is a function with equation

$v(t)={\begin{cases}v(t)={\frac {L}{1+e^{-k(t-t_{0})}}}&&{\text{if }}t<t_{0}\\L&&{\text{if }}t\geq t_{0}\end{cases}}$

where $t_{0}$ is the $t$ value of the sigmoid's midpoint, $L$ is the curve's maximum value and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is the curve's growth rate. See the Desmos graph.

The bumb function

The Bumb Function.

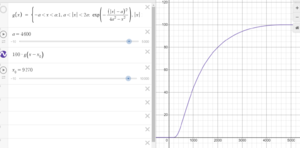
There exists some well-known every-where differentiable functions, with a compact support. One example is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_1(t) = \begin{cases} 1 &&\text{if } -a < t < a \\ e^{- \frac{(|t|-a)^2}{4a^2-t^2} } &&\text{if } a \leq |t| \\ 0 &&\text{if } t> 2a \end{cases} }

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(t) = 100 v_1(t-180)} . This is an example of a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C^\infty} with support in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a-r \leq t \leq a+r} . We are going to take half of the curve to be our velocity function. The graph is shown on Desmos page.

See more about the function at Math Stack Exchange, and the references therein.

Example Codes

First, we use Python on computer to check the scripts of the acceleration functions. These functions are applied in the motor control part. The robot script logs the data, and the data is uploaded to the computer and analyzed later.

Python

import math

def vlin(t):
    L = 100
    t0= 5000
    if t > t0:
        return L
    if t < 0:
        return 0
    return L*t/t0

def vsin(t):
    L = 100
    t0= 5000
    if t > t0:
        return L
    if t < 0:
        return 0
    return L/2*( math.sin(3.14159*t/t0-3.14159/2)+1)
    
def vlog(t):
    L = 100
    t0= 5000
    if t > t0:
        return L
    if t < 0:
        return 0
    return L/(1 + math.exp(-0.00322*(t-2500)))

def vbum(t):
    L = 100
    a = 4600
    t1= 9270
    if t > a:
        return L
    if t < 100:
        return 0
    else:
        return L*math.exp(-((t1-t)-a)**2/(4*a**2 - (t-t1)**2) )

Analysis Scripts

Note that