Eksperimentti: hyppykorkeuden määrittäminen lentoajalla.: Difference between revisions
(→Theory) |
(→Theory) |
||
| Line 7: | Line 7: | ||
== Theory == | == Theory == | ||
[[File:ForcePlate jumping2 timeOfFlight.svg|thumb]] | |||
<math>s = s_0 + v_0 t + \tfrac12 at^2</math> and thus we have <math>h = v_0 t - \tfrac12 gt^2</math> because <math>h_0=0</math> and <math>a=-g = -9.81m/s^2</math>. However, for the velocity we have <math>v = v_0 - gt</math> and at the maximum height we have that <math>v=0</math>, and thus <math>v_0 = gt_m</math> which. Combining these two we have | <math>s = s_0 + v_0 t + \tfrac12 at^2</math> and thus we have <math>h = v_0 t - \tfrac12 gt^2</math> because <math>h_0=0</math> and <math>a=-g = -9.81m/s^2</math>. However, for the velocity we have <math>v = v_0 - gt</math> and at the maximum height we have that <math>v=0</math>, and thus <math>v_0 = gt_m</math> which. Combining these two we have | ||
| Line 21: | Line 21: | ||
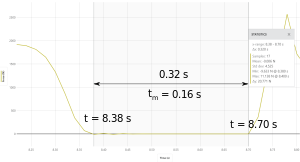
The time at the maximum height (<math>t_m</math>) will be half of the flight time. | The time at the maximum height (<math>t_m</math>) will be half of the flight time. | ||
In the experiment, we have <math>t_m = 0.16</math> s, which gives <math> h = \tfrac12 gt_m^2 = \frac12 \times 9.81 \times 0.16^2 = 0.13</math> m. | |||
Also take-off velocity is easy to calculate as a difference. | Also take-off velocity is easy to calculate as a difference. | ||
Revision as of 16:53, 3 May 2022
Introduction

Jumping on the force plate you can feel the force. We use time of flight method to estimate the height of the jump.
Theory
and thus we have because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_0=0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=-g = -9.81m/s^2} . However, for the velocity we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = v_0 - gt} and at the maximum height we have that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=0} , and thus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_0 = gt_m} which. Combining these two we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} h &= v_0 t - \tfrac12 gt^2 \\ &= gt_m^2 - \tfrac12 gt_m^2 \\ &= \tfrac12 gt_m^2 \end{matrix} }
The time at the maximum height (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_m} ) will be half of the flight time.
In the experiment, we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_m = 0.16} s, which gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = \tfrac12 gt_m^2 = \frac12 \times 9.81 \times 0.16^2 = 0.13} m.
Also take-off velocity is easy to calculate as a difference.

