The travelling salesman problem: Difference between revisions
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
The travelling salesman problem is a legendary math problem. The question is, how to find the shortest path to visit all the given cities and to come back home. To make the game interesting, many cities are needed, and thus a rather large floor area. | |||
[[File:Capitals.pdf|thumb|The capitals are downloadable here as capitals.pdf -> original file.]] | |||
=== Aim === | === Aim === | ||
Distance, time. Geography and energy. | |||
== Robot == | == Robot == | ||
Almost any robot will do, though we use Asimov 2/ Verne robot. | |||
=== Sensors === | === Sensors === | ||
No sensors are used, except the servo motors. | |||
== Example Video == | == Example Video == | ||
<youtube>yVxRwXJA9e4</youtube> | |||
== Theory == | == Theory == | ||
Write (or print) the names of cities (eg. European capitals) into papers. The Wikipedia page includes 50 countries, and that might be too much, but choose 7 to 15 cities to be distributed and taped onto the floor. | |||
Using only green <code>steering</code> blocks, try to visit as many cities as possible, and minimizing the travel distance or travelling time. | |||
== Example Code == | |||
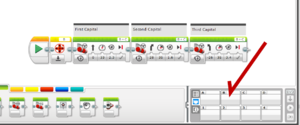
The following code visits three Capitals but does not return home after the trip. In the beginning, the motor rotation is reset such that the total rotation of motor B can read from the program, see the red arrow. | |||
[[File:TravellingSalesman.png|thumb]] | |||
== Exercises == | == Exercises == | ||
* Visit 10 cities. Consider first what is the optimal route to minimize the travel. Note that after visiting multiple cities, the orientation of robot becomes wobbly. | |||
* Print the total distance (of motor B) onto screen. | |||
* Use the [[How to use gyroscope|gyroscope]] the fix the uncertainty with the direction. | |||
* Try to minimize the time used to travel all the cities. Print the elapsed time onto screen. | |||
Back to [[Mahtavaa Matematiikkaa 2020]] | Back to [[Mahtavaa Matematiikkaa 2020]] | ||
[[File:Mahtavaa matematiikkaa.png|thumb]] | [[File:Mahtavaa matematiikkaa.png|thumb]] | ||
Latest revision as of 00:18, 19 October 2020
Introduction
The travelling salesman problem is a legendary math problem. The question is, how to find the shortest path to visit all the given cities and to come back home. To make the game interesting, many cities are needed, and thus a rather large floor area.

Aim
Distance, time. Geography and energy.
Robot
Almost any robot will do, though we use Asimov 2/ Verne robot.
Sensors
No sensors are used, except the servo motors.
Example Video
Theory
Write (or print) the names of cities (eg. European capitals) into papers. The Wikipedia page includes 50 countries, and that might be too much, but choose 7 to 15 cities to be distributed and taped onto the floor.
Using only green steering blocks, try to visit as many cities as possible, and minimizing the travel distance or travelling time.
Example Code
The following code visits three Capitals but does not return home after the trip. In the beginning, the motor rotation is reset such that the total rotation of motor B can read from the program, see the red arrow.
Exercises
- Visit 10 cities. Consider first what is the optimal route to minimize the travel. Note that after visiting multiple cities, the orientation of robot becomes wobbly.
- Print the total distance (of motor B) onto screen.
- Use the gyroscope the fix the uncertainty with the direction.
- Try to minimize the time used to travel all the cities. Print the elapsed time onto screen.
Back to Mahtavaa Matematiikkaa 2020
