Basics of Structural Analysis: Difference between revisions
| (7 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
Structural analysis using about high school level physics and maths. | Structural analysis using about high school level physics and maths. | ||
The terms used | |||
* <math>E</math> Young's modulus <math>\sigma = E\epsilon</math> is to be compared to <math>F= kx</math> | |||
* <math>\sigma</math> is the stress (force) in the material. It is defined as <math>\sigma = \frac{F}{A}</math> | |||
* <math>\sigma_{cr}</math> Critical stress. | |||
* <math>\sigma_{cr}</math> | |||
* <math>\sigma_{cr}</math> | |||
* <math>\sigma_{cr}</math> | |||
* <math>\epsilon</math> is the strain or deformation (displacement) in the object (perhaps in the dimension of length ratio): <math>\epsilon = \frac{\partial}{\partial X}(x-X)= F'-I</math> where <math>X</math> is the reference position of material. For a uniform bar <math>\epsilon = \frac{\Delta L}{L} = \frac{\sigma}{E} = \frac{F}{AE}</math>. | |||
* <math>\lambda</math> is the stretch ratio: <math>\lambda = \frac{L+\Delta L}{L}</math> | |||
* <math>\nu</math> Poisson ratio is a measure of deformation of material. <math>\nu = - \frac{d \epsilon_y}{d \epsilon_x}</math> | |||
* <math></math> | |||
== Basic theory == | == Basic theory == | ||
| Line 71: | Line 82: | ||
== Cylindrical Pipe == | == Cylindrical Pipe == | ||
[[File:AxialStress.svg|thumb|Axial stress]] | |||
Cylinder stress | Cylinder stress | ||
| Line 79: | Line 92: | ||
=== Axial stress === | === Axial stress === | ||
The axial stress is uniform across the cylinder wall. The stress is found by equilibrium calculations (see below). See the difference between external and internal pressure. | The axial stress is uniform across the cylinder wall. The stress is found by equilibrium calculations (see below). See the difference between external and internal pressure. | ||
'''External pressure''' | |||
The critical stress is <math>\sigma_{cr} = \frac{F}t = \frac{RE}{S(1-\nu^2)}</math>, where <math>E</math> is the Young's modulus, <math>\nu</math> is the Poisson ratio, <math>R</math> is the radius of the shell and . . .[Not ok. . . , see https://core.ac.uk/download/pdf/10851171.pdf page 28. ] | |||
'''Internal pressure''' | |||
The force <math>p_iA_i</math> from the internal pressure is equilibrated by the wall stress <math>\sigma_a A_a = \sigma_a (A_o - A_i)</math> where <math>A_i</math> is internal area and <math>A_o</math> is the outer area. | |||
The force on the direction of axis (from center to the loop) due to the pressure is | The force on the direction of axis (from center to the loop) due to the internal pressure is | ||
<math> | <math> | ||
F = \int_0^r 2 p \pi r dr = 2 p \pi \frac{r^2}{2} = p \pi \frac{D^2}{4} | F = \int_0^r 2 p \pi r dr = 2 p \pi \frac{r^2}{2} = p \pi \frac{D^2}{4} | ||
Latest revision as of 09:19, 23 January 2024
Introduction
Structural analysis using about high school level physics and maths.
The terms used
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} Young's modulus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = E\epsilon} is to be compared to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F= kx}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is the stress (force) in the material. It is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{F}{A}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{cr}} Critical stress.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{cr}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{cr}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{cr}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} is the strain or deformation (displacement) in the object (perhaps in the dimension of length ratio): Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \frac{\partial}{\partial X}(x-X)= F'-I} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} is the reference position of material. For a uniform bar Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \frac{\Delta L}{L} = \frac{\sigma}{E} = \frac{F}{AE}} .
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} is the stretch ratio: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = \frac{L+\Delta L}{L}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} Poisson ratio is a measure of deformation of material. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu = - \frac{d \epsilon_y}{d \epsilon_x}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle }
Basic theory
Principle of superposition: linearity. Displacement at location Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} from forces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_1} and </math>P_2</math> located at different positions is calculated as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_B = \Delta_{BP_1} + \Delta_{BP_2}}
The energy principle: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dW = Fd\Delta} giving the total energy as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_0^\Delta Fd\Delta} which is called strain energy. For linear deformation this gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\tfrac12 F\Delta} .
Virtual work principle.
Dead loads, live loads, impact loads (impact factor), wind loads.
Equilibrium.
Forces:
- Normal force and axial force (out-of-plane forces, in-plane forces)
- Shearing force Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{V(x)}{x} = -w(x) } . Thus we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta V =\int w(x) dx } . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(x)} is the intensity of applied (normal?) force.
- Bending moment Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dM}{dx} = V(x)} and thus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2M}{dx^2} = -w(x)} .
- Torsion (of a plate)
- Curvature and twist
Hooke's law hold for linear elastic material: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \frac{\sigma}{E}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is the bending stress. The force Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta P} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta P = \sigma \delta A} . Yield point (strength) is when Hooke's law is not acceptable anymore; the limit of elastic behavior. It is often used to determine the maximum allowable load in the component.
Buckling is a process by which a structure cannot withstand loads so it must change its shape. Stable equilibrium is when the force (pressure) applied doesn't reach the critical load, allowing the structure to return to its original equilibrium.
Plate
- Torsion (of a plate)
- Curvature and twist Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{xy}} .
Curvature in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_x = \frac1{R_x}} is the rate of change of the slope with respect to arch length, giving Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_x = \frac{\frac{\partial^2 w}{\partial x^2}} {\sqrt{(1 + \left(\frac{\partial w}{\partial x} \right)^2}^3} }
Strains in a plate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{xx}}
.
Von Kármán strains.
Beam
Forces:
- Normal force and axial force
- Shearing force Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{V(x)}{x} = -w(x) } . Thus we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta V =\int w(x) dx } . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(x)} is the intensity of applied (normal?) force.
- Bending moment Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dM}{dx} = V(x)} and thus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2M}{dx^2} = -w(x)} .
Deflection of beams

The strain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} in the filament is due to the different lengths of filaments in bended beam. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \frac{\ell_1 - \ell}{\ell} = \frac{\Delta y}{R}} which for linear elastic material (using Hooke's law) gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac\sigma E = \frac{\Delta y}{R} = \epsilon} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is bending stress
Radius of curvature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac1R = \frac{\partial v^2}{\partial x^2}}
, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{xx} = -y \frac{\partial^2 v}{\partial x^2}}
.
Column
Column is a vertical beam.
Cylindrical Pipe
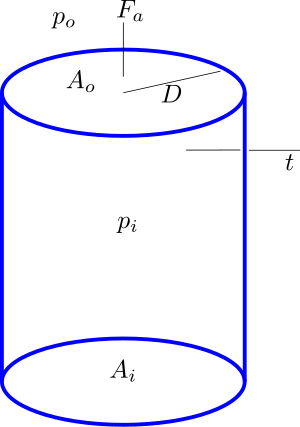
Cylinder stress
- Axial (Longitudinal) stress Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_a}
- Tangential (hoop or circumferential) stress Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_t}
- Radial stress Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_r}
Axial stress
The axial stress is uniform across the cylinder wall. The stress is found by equilibrium calculations (see below). See the difference between external and internal pressure.
External pressure
The critical stress is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{cr} = \frac{F}t = \frac{RE}{S(1-\nu^2)}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is the Young's modulus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} is the Poisson ratio, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} is the radius of the shell and . . .[Not ok. . . , see https://core.ac.uk/download/pdf/10851171.pdf page 28. ]
Internal pressure
The force Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_iA_i} from the internal pressure is equilibrated by the wall stress Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_a A_a = \sigma_a (A_o - A_i)} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_i} is internal area and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_o} is the outer area.
The force on the direction of axis (from center to the loop) due to the internal pressure is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = \int_0^r 2 p \pi r dr = 2 p \pi \frac{r^2}{2} = p \pi \frac{D^2}{4} }
The axial stress is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_L = \frac{F}{A} = \frac{p\pi \frac{D^2}{4} }{\pi D t} = \frac{pD}{4t}}
The pressure effect
The longitudinal stress and hoop (radial) stress.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_L = \frac{pD}{4t}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p}
is the internal pressure, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D}
is the mean diameter of cylinder and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t}
is the wall thickness. Also, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_H = \frac{pD}{2t}}
.
Applying Hooke's law and the fact that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_H = 2\sigma_L} we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_L = \frac{\epsilon_L + v\epsilon_H}{1-\nu^2}E = \frac{\epsilon_H}{2-\nu}E }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} is the Poisson's ratio and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is the Young's modulus.
Buckling of cylinders
The differential equation of the classical buckling theory of a thin-walled shell. . .
Analytic solution.
Fiberglass (Glassfiber) Cansat
Also impact strength should be considered as the explosion is hard.
The stress is in general defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac FA} . However, the area changes (usually grows: spreads laterally) while compressing. While in Hooke's regime, we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = E\epsilon} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is Young's modulus and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} is the strain (deformation) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \frac{\Delta \ell}{\ell}} . In this region the material deforms elastically and returns to its original shape.
The longitudinal stress of cylindrical pipe is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_L = \frac{F}{4t}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} is the applied force, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is the Young's modulus.
The diameter of the cansat can is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=66} mm. Thickness Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} is to be determined. The force Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} acting on the soda can when the payload is ejected from the rocket is CHECK this Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=700} N.
Thus, we will have for the thickness Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \frac{F}{4\sigma_L} = frac{700 N}{4}} .
Compressive stress is the capacity of a material to withstand loads tending to reduce size.
Fibreglass is fibre-reinforced plastic, in which the fibres originates from glass, carbon, aramid or basalt, usually. The polymer is usually an epoxy, vinyl ester or resin (hartsi in Finnish, vaik in Estonian). The polyester resin is liquid, which will solidify when the hardener is added. The hardener (Methyl Ethyl Ketone Peroxide).
However, below is structural properties of glass fiber. Normal glass fiber is E-glass, which is alumino-borosilicate glass with less than 1% alkali oxides. See more details at https://kevra.fi/?s=lasikuitu or https://composite24.ee/tooted/kangas-ja-kiud
| Tensile strength [MPa] | Compressive strength [MPa] | Yield strength [Mpa] | Ultimate strength [Mpa] | Young's modulus E [GPa] | Density g/cm3 | |
|---|---|---|---|---|---|---|
| E glass | 3445 | 1080 | - | 5650 | 76 | 2.58 |
| Unsaturated polyester | 90 | 55 | 3.23 | 1.35 | ||
| Epoxy | - | 26-85 | 3 | 1.35 | ||
| S-2 | 4890 | 1600 | 85.5 |
The fiber is usually made to be a fabric or mat (or more).
- Thickness of the fabric is between 0.04 mm and 0.23, usually.
References
https://tiij.org/issues/issues/spring2006/12_Dues-Accepted/Dues.pdf
https://core.ac.uk/download/pdf/10851171.pdf
https://www.sciencedirect.com/science/article/abs/pii/S0263823101000660 Paywall
Mechanical Properties of Glass Fiber Reinforced Polyester Composites
https://www.engineeringtoolbox.com/young-modulus-d_417.html#gsc.tab=0 The table for strengths.
http://k-mac-plastics.com/data-sheets/fiberglass_technical_data.htm