Grover's Algorithm: Difference between revisions
| (19 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
Apply an other reflection about the state <math>|u\rangle</math>, also <math>U_u = 2 |u\rangle \langle u| - 1</math>. Thus we are at state <math>U_u U_w |u></math>. This amplifies by two the amplitude of state <math>|w\rangle</math>. | Apply an other reflection about the state <math>|u\rangle</math>, also <math>U_u = 2 |u\rangle \langle u| - 1</math>. Thus we are at state <math>U_u U_w |u></math>. This amplifies by two the amplitude of state <math>|w\rangle</math>. | ||
Repeat <math>t< | Repeat <math>t</math> times, where <math>t\approx \sqrt N</math>. | ||
== Application: Lights Out == | |||
[[File:LightsOut.png|thumb]] | |||
We solve the <math>3\times3</math> tiling game using superposition (instead of Gaussian elimination). The algorithm finds the N-qubit for which the initial state becomes zero. | |||
First, the numbering system is shown below: | |||
{| class="wikitable" | |||
|- | |||
| 0 || 1 || 2 | |||
|- | |||
| 3 || 4 || 5 | |||
|- | |||
| 6 || 7 || 8 | |||
|} | |||
Second, we need a function that flips the lights: By pressing 0 the light in cells {0, 1, 3} will toggle. Thus the toggle mapping is: | |||
* 0 -> {0, 1, 3} | |||
* 1 -> {0, 1, 2, 4} | |||
* 2 -> {1, 2, 5} | |||
* 3 -> {0, 3, 4, 6} | |||
* 4 -> {1, 3, 4, 5, 7} | |||
* 5 -> {2, 4, 5, 8} | |||
* 6 -> {3, 6, 7} | |||
* 7 -> {4, 6, 7, 8} | |||
* 8 -> {5, 7, 8} | |||
The diffusion (Amplification) part is the most difficult. | |||
Solution space is <math>2^9=512</math>, the optimal number of iteration is about <math>\frac{\pi}{4} \sqrt{2^9} - \frac{1}{2} \approx 17.3 \approx 17</math>. | |||
<syntaxhighlight> | |||
lights = [0, 0, 0, | |||
0, 1, 1, | |||
0, 1, 0] | |||
def map_board(lights, qc, qr): | |||
j = 0 | |||
for i in lights: | |||
if i==1: | |||
qc.x(qr[j]) | |||
j+=1 | |||
else: | |||
j+=1 | |||
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister | |||
tile = QuantumRegister(9) | |||
flip = QuantumRegister(9) | |||
oracle = QuantumRegister(1) | |||
result = ClassicalRegister(9) | |||
#19=9+9+1 qubit + 4bit | |||
qc = QuantumCircuit(oracle, tile, flip, result) | |||
def initialize(): | |||
map_board(lights, qc, tile) | |||
qc.h(flip[:]) | |||
qc.x(oracle[0]) | |||
qc.h(oracle[0]) #Hadamard superposition | |||
# Subroutine for oracle | |||
def flip_tile(qc,flip,tile): | |||
qc.cx(flip[0], tile[0]) | |||
qc.cx(flip[0], tile[1]) | |||
qc.cx(flip[0], tile[3]) | |||
qc.cx(flip[1], tile[0]) | |||
qc.cx(flip[1], tile[1]) | |||
qc.cx(flip[1], tile[2]) | |||
qc.cx(flip[1], tile[4]) | |||
qc.cx(flip[2], tile[1]) | |||
qc.cx(flip[2], tile[2]) | |||
qc.cx(flip[2], tile[5]) | |||
qc.cx(flip[3], tile[0]) | |||
qc.cx(flip[3], tile[3]) | |||
qc.cx(flip[3], tile[4]) | |||
qc.cx(flip[3], tile[6]) | |||
qc.cx(flip[4], tile[1]) | |||
qc.cx(flip[4], tile[3]) | |||
qc.cx(flip[4], tile[4]) | |||
qc.cx(flip[4], tile[5]) | |||
qc.cx(flip[4], tile[7]) | |||
qc.cx(flip[5], tile[2]) | |||
qc.cx(flip[5], tile[4]) | |||
qc.cx(flip[5], tile[5]) | |||
qc.cx(flip[5], tile[8]) | |||
qc.cx(flip[6], tile[3]) | |||
qc.cx(flip[6], tile[6]) | |||
qc.cx(flip[6], tile[7]) | |||
qc.cx(flip[7], tile[4]) | |||
qc.cx(flip[7], tile[6]) | |||
qc.cx(flip[7], tile[7]) | |||
qc.cx(flip[7], tile[8]) | |||
qc.cx(flip[8], tile[5]) | |||
qc.cx(flip[8], tile[7]) | |||
qc.cx(flip[8], tile[8]) | |||
def all_zero(qc, tile): | |||
qc.x(tile[0:9]) | |||
qc.mct(tile[0:9], oracle[0]) | |||
qc.x(tile[0:9]) | |||
# create the circuit | |||
initialize() | |||
qc.barrier() | |||
for i in range(17): | |||
# oracle | |||
flip_tile(qc,flip,tile) | |||
qc.barrier() | |||
all_zero(qc, tile) | |||
qc.barrier() | |||
# U^dagger of flip_tile. | |||
flip_tile(qc,flip,tile) | |||
qc.barrier() | |||
# diffusion | |||
qc.h(flip) | |||
qc.x(flip) | |||
qc.h(flip[8]) | |||
qc.mct(flip[0:8], flip[8]) | |||
qc.h(flip[8]) | |||
qc.x(flip) | |||
qc.h(flip) | |||
qc.barrier() | |||
# Uncompute | |||
qc.h(oracle[0]) | |||
qc.x(oracle[0]) | |||
qc.barrier() | |||
# Measurement | |||
qc.measure(flip,result) | |||
qc.barrier() | |||
# Make the output order the same as the input. | |||
qc = qc.reverse_bits() | |||
from qiskit import execute, Aer | |||
backend = Aer.get_backend('statevector_simulator') | |||
job = execute(qc,backend) | |||
result = job.result() | |||
count = result.get_counts() | |||
score_sorted = sorted(count.items(), key=lambda x:x[1], reverse=True) | |||
final_score = score_sorted[0:20] | |||
print( final_score ) | |||
</syntaxhighlight> | |||
The example above is very low and inefficient. It can be sped up. | |||
=== References === | === References === | ||
https://medium. | https://mathworld.wolfram.com/LightsOutPuzzle.html | ||
http://perfectweb.org/ddo/solver/vale_puzzle.html | |||
https://gaming.stackexchange.com/questions/11123/strategy-for-solving-lights-out-puzzle | |||
https://github.com/qiskit-community/IBMQuantumChallenge2020/blob/main/hints/hint_2a_nb/hint_2a_ex.ipynb | |||
== References == | |||
https://medium.om/swlh/grovers-algorithm-quantum-computing-1171e826bcfb | |||
https://quantumcomputinguk.org/tutorials/grovers-algorithm-with-code | https://quantumcomputinguk.org/tutorials/grovers-algorithm-with-code | ||
https://jonathan-hui.medium.com/qc-grovers-algorithm-cd81e61cf248 | https://jonathan-hui.medium.com/qc-grovers-algorithm-cd81e61cf248 | ||
https://arxiv.org/pdf/1804.03719.pdf | |||
https://www.quantum-inspire.com/kbase/grover-algorithm/ | |||
http://davidbkemp.github.io/animated-qubits/grover.html | |||
https://quantum-computing.ibm.com/docs/iqx/guide/grovers-algorithm | |||
https://qudev.phys.ethz.ch/static/content/courses/QSIT12/presentations/Grover_superconducting.pdf | |||
https://quantumcomputing.stackexchange.com/questions/2110/grovers-algorithm-where-is-the-list | |||
https://qudev.phys.ethz.ch/static/content/QSIT16/talks/Grover_QSIT.pdf | |||
https://grove-docs.readthedocs.io/en/latest/grover.html | |||
https://thequantumdaily.com/2019/11/13/quantum-programming-101-grovers-algorithm/ | |||
Latest revision as of 11:55, 29 November 2020
Introduction
Theory
Oracle Function
Amplitude Amplification
The uniform superposition: , where is the Hadamard gate.
Apply the oracle reflection .
Apply an other reflection about the state , also . Thus we are at state . This amplifies by two the amplitude of state .
Repeat times, where .
Application: Lights Out
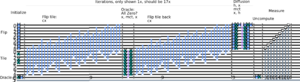
We solve the tiling game using superposition (instead of Gaussian elimination). The algorithm finds the N-qubit for which the initial state becomes zero.
First, the numbering system is shown below:
| 0 | 1 | 2 |
| 3 | 4 | 5 |
| 6 | 7 | 8 |
Second, we need a function that flips the lights: By pressing 0 the light in cells {0, 1, 3} will toggle. Thus the toggle mapping is:
- 0 -> {0, 1, 3}
- 1 -> {0, 1, 2, 4}
- 2 -> {1, 2, 5}
- 3 -> {0, 3, 4, 6}
- 4 -> {1, 3, 4, 5, 7}
- 5 -> {2, 4, 5, 8}
- 6 -> {3, 6, 7}
- 7 -> {4, 6, 7, 8}
- 8 -> {5, 7, 8}
The diffusion (Amplification) part is the most difficult.
Solution space is , the optimal number of iteration is about .
lights = [0, 0, 0,
0, 1, 1,
0, 1, 0]
def map_board(lights, qc, qr):
j = 0
for i in lights:
if i==1:
qc.x(qr[j])
j+=1
else:
j+=1
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
tile = QuantumRegister(9)
flip = QuantumRegister(9)
oracle = QuantumRegister(1)
result = ClassicalRegister(9)
#19=9+9+1 qubit + 4bit
qc = QuantumCircuit(oracle, tile, flip, result)
def initialize():
map_board(lights, qc, tile)
qc.h(flip[:])
qc.x(oracle[0])
qc.h(oracle[0]) #Hadamard superposition
# Subroutine for oracle
def flip_tile(qc,flip,tile):
qc.cx(flip[0], tile[0])
qc.cx(flip[0], tile[1])
qc.cx(flip[0], tile[3])
qc.cx(flip[1], tile[0])
qc.cx(flip[1], tile[1])
qc.cx(flip[1], tile[2])
qc.cx(flip[1], tile[4])
qc.cx(flip[2], tile[1])
qc.cx(flip[2], tile[2])
qc.cx(flip[2], tile[5])
qc.cx(flip[3], tile[0])
qc.cx(flip[3], tile[3])
qc.cx(flip[3], tile[4])
qc.cx(flip[3], tile[6])
qc.cx(flip[4], tile[1])
qc.cx(flip[4], tile[3])
qc.cx(flip[4], tile[4])
qc.cx(flip[4], tile[5])
qc.cx(flip[4], tile[7])
qc.cx(flip[5], tile[2])
qc.cx(flip[5], tile[4])
qc.cx(flip[5], tile[5])
qc.cx(flip[5], tile[8])
qc.cx(flip[6], tile[3])
qc.cx(flip[6], tile[6])
qc.cx(flip[6], tile[7])
qc.cx(flip[7], tile[4])
qc.cx(flip[7], tile[6])
qc.cx(flip[7], tile[7])
qc.cx(flip[7], tile[8])
qc.cx(flip[8], tile[5])
qc.cx(flip[8], tile[7])
qc.cx(flip[8], tile[8])
def all_zero(qc, tile):
qc.x(tile[0:9])
qc.mct(tile[0:9], oracle[0])
qc.x(tile[0:9])
# create the circuit
initialize()
qc.barrier()
for i in range(17):
# oracle
flip_tile(qc,flip,tile)
qc.barrier()
all_zero(qc, tile)
qc.barrier()
# U^dagger of flip_tile.
flip_tile(qc,flip,tile)
qc.barrier()
# diffusion
qc.h(flip)
qc.x(flip)
qc.h(flip[8])
qc.mct(flip[0:8], flip[8])
qc.h(flip[8])
qc.x(flip)
qc.h(flip)
qc.barrier()
# Uncompute
qc.h(oracle[0])
qc.x(oracle[0])
qc.barrier()
# Measurement
qc.measure(flip,result)
qc.barrier()
# Make the output order the same as the input.
qc = qc.reverse_bits()
from qiskit import execute, Aer
backend = Aer.get_backend('statevector_simulator')
job = execute(qc,backend)
result = job.result()
count = result.get_counts()
score_sorted = sorted(count.items(), key=lambda x:x[1], reverse=True)
final_score = score_sorted[0:20]
print( final_score )The example above is very low and inefficient. It can be sped up.
References
https://mathworld.wolfram.com/LightsOutPuzzle.html
http://perfectweb.org/ddo/solver/vale_puzzle.html
https://gaming.stackexchange.com/questions/11123/strategy-for-solving-lights-out-puzzle
References
https://medium.om/swlh/grovers-algorithm-quantum-computing-1171e826bcfb
https://quantumcomputinguk.org/tutorials/grovers-algorithm-with-code
https://jonathan-hui.medium.com/qc-grovers-algorithm-cd81e61cf248
https://arxiv.org/pdf/1804.03719.pdf
https://www.quantum-inspire.com/kbase/grover-algorithm/
http://davidbkemp.github.io/animated-qubits/grover.html
https://quantum-computing.ibm.com/docs/iqx/guide/grovers-algorithm
https://qudev.phys.ethz.ch/static/content/courses/QSIT12/presentations/Grover_superconducting.pdf
https://quantumcomputing.stackexchange.com/questions/2110/grovers-algorithm-where-is-the-list
https://qudev.phys.ethz.ch/static/content/QSIT16/talks/Grover_QSIT.pdf
https://grove-docs.readthedocs.io/en/latest/grover.html
https://thequantumdaily.com/2019/11/13/quantum-programming-101-grovers-algorithm/











