Numerical integration and differentation in the PID algorithm: Difference between revisions
| (16 intermediate revisions by the same user not shown) | |||
| Line 17: | Line 17: | ||
A light sensor is used. | A light sensor is used. | ||
== Example Video == | == Example Video == | ||
<youtube>du3D7S2Ea3U</youtube> | |||
== Theory == | == Theory == | ||
| Line 29: | Line 31: | ||
| Error || <math>\epsilon</math> || Sensor value - target value | | Error || <math>\epsilon</math> || Sensor value - target value | ||
|- | |- | ||
| Integral || <math>I</math> || Integral + error | | Integral || <math>I</math> || <math>\alpha\times</math>Integral + error | ||
|- | |- | ||
| Derivative || <math>D</math> || Error - previous error | | Derivative || <math>D</math> || Error - previous error | ||
|} | |} | ||
Steering is | Steering is <math>S = K_p \epsilon + K_i I + K_d D </math>. The parameter <math>\alpha</math> is to ensure that the old data is forgotten and the robot relays on a rather new historical data, only. | ||
<math>S = K_p \epsilon + K_i I + K_d D </math>. | |||
We use three different parameters <math>K_p</math>, <math>K_i</math> and <math>K_d</math>. Furthermore, the integral needs to forget the very old data, and thus we need an <math>\alpha</math> term (which can be multiplied together to <math>K_i</math> already). Of course, the parameters depend on the line and robot. | We use three different parameters <math>K_p</math>, <math>K_i</math> and <math>K_d</math>. Furthermore, the integral needs to forget the very old data, and thus we need an <math>\alpha</math> term (which can be multiplied together to <math>K_i</math> already). Of course, the parameters depend on the line and robot. | ||
| Line 44: | Line 45: | ||
Set the folders properly and by pressing [[Install ev3dev|F5]] the script will run. | Set the folders properly and by pressing [[Install ev3dev|F5]] the script will run. | ||
<syntaxhighlight lang="python"> | |||
#!/usr/bin/env python3 | |||
# https://sites.google.com/site/ev3devpython/ | |||
#84 is Max | |||
#5 is Min | |||
from ev3dev2.sensor.lego import ColorSensor | |||
from ev3dev2.motor import MoveSteering, OUTPUT_B, OUTPUT_C | |||
import os | |||
os.system('setfont Lat15-TerminusBold32x16') | |||
import csv | |||
f = open("steering.csv","w") | |||
writer = csv.writer(f) | |||
steer_pair = MoveSteering(OUTPUT_B, OUTPUT_C) | |||
cl = ColorSensor() | |||
clMax = 84 | |||
clMin = 5 | |||
clAve = (clMax + clMin)/2 | |||
Kp= .5 | |||
Ki= 0.4 | |||
Kd= 1.4 | |||
alpha = 0.8 | |||
clN = clAve | |||
steering = 0 | |||
integral = 0 | |||
derivative = 0 | |||
error_prev = 0 | |||
while clN < 95: | |||
clN = cl.reflected_light_intensity | |||
error = ( clN - clAve ) | |||
integral = alpha*integral + error | |||
derivative = error - error_prev | |||
error_prev = error | |||
error = Kp*error | |||
writer.writerow(( error, Ki*integral, Kd*derivative) ) | |||
steering = error + Ki*integral + Kd*derivative | |||
steering = min(steering, 100) | |||
steering = max(steering, -100) | |||
print( clN ) | |||
steer_pair.on(steering=steering, speed=-20) | |||
steer_pair.off() | |||
f.close() | |||
</syntaxhighlight> | |||
=== Python analysis on a computer === | === Python analysis on a computer === | ||
[[File:PID analysis.png|thumb|PID Analysis. The integral part cumulates, and the derivatives accounts for the rapid change in reflectance.]] | |||
[[File:PID_Ki=Kd=0.png|thumb|PID Analysis of proportional line follower, thus <math>K_i=0</math> and <math>K_d=0</math>.]] | |||
Adjusting the parameters without any guidance is rather difficult. To set up the parameters we use an other python script that plots the data. The idea is to have absolute value of total steering less than 100, or perhaps even more smaller. The smaller steering value, the less the robot deviates. First, set one of the three parameters to zero, and adjust two of them. Then adjust the third one, by modifying the other two. | |||
<syntaxhighlight lang="python"> | |||
import matplotlib.pyplot as plt | |||
import pandas as pd | |||
df = pd.read_csv('C:/Users/markkuleino/Downloads/steering.csv', names=["error", "integral", "derivative"]) | |||
df["steering"] = df.sum(axis=1) | |||
ls = ['r-', 'g-', 'b-', 'k--'] | |||
df.plot( style = ls ) | |||
</syntaxhighlight> | |||
== Exercises == | == Exercises == | ||
* Draw a 50 cm long straight line and adjust the parameters such that the robot follows smoothly the line. As a first approximation the line should be symmetric, that the black line is very thick. | |||
* Draw a straight line with two curves and adjust the parameters so that the robot drives smoothly along the line. Make a line with straight section and smooth curves with a small radius. | |||
* Check the meaning of each parameters <math>K_p</math>, <math>K_i</math>, <math>K_d</math> and <math>\alpha</math>. Tabulate the results. | |||
* Define a measure to quantitively check which set of parameters are the best ones. A good measure might be (1) time to run the line, (2) estimate the smoothness of the path of the robot (using the second numerical differential of logged steering value, and summing over the absolute value of that). | |||
== References == | == References == | ||
Latest revision as of 20:57, 18 October 2020
Introduction
PID is elaborated algorithm to use in numerous ways. Though it might difficult to set up the parameters correctly, it makes the robot move more smoothly and thus more rapid. The P is for Proportional, I is the Integral and D is Differential. We use PID in line following.
Aim
Proportion, Integration and Derivation.
Plotting, Error function.
Robot
Almost any robot will do, but we will use Asimov 2/ Verne robot.
Sensors
A light sensor is used.
Example Video
Theory
If applying only proportional coding, the steering is affected by the amount of difference in reflectance from the average. The integral term is a sum (or integral) of the previous (historical) errors, and that is used to correct steering if it has been wrong for a while. The differential is used to forecast the next error based on the previous errors, and we use it to steer more or less depending on the previous error.
| Term | Math | Meaning |
|---|---|---|
| Error | Sensor value - target value | |
| Integral | Integral + error | |
| Derivative | Error - previous error |
Steering is . The parameter is to ensure that the old data is forgotten and the robot relays on a rather new historical data, only.
We use three different parameters , and . Furthermore, the integral needs to forget the very old data, and thus we need an term (which can be multiplied together to already). Of course, the parameters depend on the line and robot.
Example Code
Python v2 Ev3dev
Set the folders properly and by pressing F5 the script will run.
#!/usr/bin/env python3
# https://sites.google.com/site/ev3devpython/
#84 is Max
#5 is Min
from ev3dev2.sensor.lego import ColorSensor
from ev3dev2.motor import MoveSteering, OUTPUT_B, OUTPUT_C
import os
os.system('setfont Lat15-TerminusBold32x16')
import csv
f = open("steering.csv","w")
writer = csv.writer(f)
steer_pair = MoveSteering(OUTPUT_B, OUTPUT_C)
cl = ColorSensor()
clMax = 84
clMin = 5
clAve = (clMax + clMin)/2
Kp= .5
Ki= 0.4
Kd= 1.4
alpha = 0.8
clN = clAve
steering = 0
integral = 0
derivative = 0
error_prev = 0
while clN < 95:
clN = cl.reflected_light_intensity
error = ( clN - clAve )
integral = alpha*integral + error
derivative = error - error_prev
error_prev = error
error = Kp*error
writer.writerow(( error, Ki*integral, Kd*derivative) )
steering = error + Ki*integral + Kd*derivative
steering = min(steering, 100)
steering = max(steering, -100)
print( clN )
steer_pair.on(steering=steering, speed=-20)
steer_pair.off()
f.close()
Python analysis on a computer
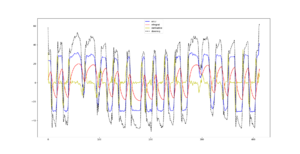
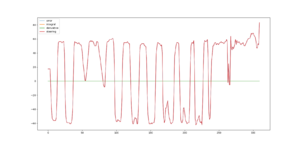
Adjusting the parameters without any guidance is rather difficult. To set up the parameters we use an other python script that plots the data. The idea is to have absolute value of total steering less than 100, or perhaps even more smaller. The smaller steering value, the less the robot deviates. First, set one of the three parameters to zero, and adjust two of them. Then adjust the third one, by modifying the other two.
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv('C:/Users/markkuleino/Downloads/steering.csv', names=["error", "integral", "derivative"])
df["steering"] = df.sum(axis=1)
ls = ['r-', 'g-', 'b-', 'k--']
df.plot( style = ls )
Exercises
- Draw a 50 cm long straight line and adjust the parameters such that the robot follows smoothly the line. As a first approximation the line should be symmetric, that the black line is very thick.
- Draw a straight line with two curves and adjust the parameters so that the robot drives smoothly along the line. Make a line with straight section and smooth curves with a small radius.
- Check the meaning of each parameters , , and . Tabulate the results.
- Define a measure to quantitively check which set of parameters are the best ones. A good measure might be (1) time to run the line, (2) estimate the smoothness of the path of the robot (using the second numerical differential of logged steering value, and summing over the absolute value of that).
References
See [PID Controller For Lego Mindstorms Robots]
Back to Mahtavaa Matematiikkaa 2020











